Предмет: Алгебра,
автор: rostislavvv77
Помогите решить систему уровнений, пожалуйста!:(
Приложения:
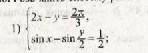
Ответы
Автор ответа:
1
Ответ:
n принадлежит Z
rostislavvv77:
ааа, спасибооо
Похожие вопросы
Предмет: Русский язык,
автор: Superboy7337
Предмет: Английский язык,
автор: kseniya2066
Предмет: Русский язык,
автор: Dazzers
Предмет: Математика,
автор: Aliniaka123451
Предмет: Математика,
автор: ррп15