Предмет: Геометрия,
автор: jamshidnurlibaev
Высота конуса равна 4, он вписан в шар,радиус которого равен 5. Найдите объём конуса
Ответы
Автор ответа:
2
Ответ:
Объяснение:
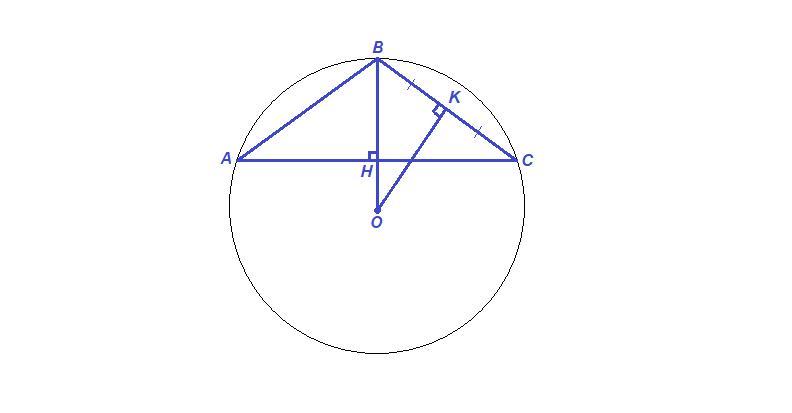
Изобразим осевое сечение конуса - равнобедренный треугольник АВС.
Сечение шара - большой круг, описанный около этого треугольника.
Центр шара - точка О - лежит в точке пересечения серединных перпендикуляров к сторонам треугольника.
ВН = 4 - высота конуса
ВО = 5 - радиус описанного шара.
Рассмотрим треугольники ВСН и ВОК:
∠ВНС = ∠ВКО = 90°,
∠В - общий, значит
ΔВСН ~ ΔВОК по двум углам.
Из подобия треугольников следует:
Учитывая, что BC = 2BK, получаем:
⇒
Из прямоугольного треугольника ВНС по теореме Пифагора:
- радиус основания конуса.
Объем конуса:
где R = CH = 2√6
h = ВН = 4
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Rauaida
Предмет: Русский язык,
автор: nastysha30
Предмет: Русский язык,
автор: burtoliks
Предмет: Другие предметы,
автор: Renatik2010
Предмет: Обществознание,
автор: sekretsekrets