Предмет: Геометрия,
автор: aczesareva
Срочно объясните номер 574!!
Приложения:

Ответы
Автор ответа:
1
Ответ:
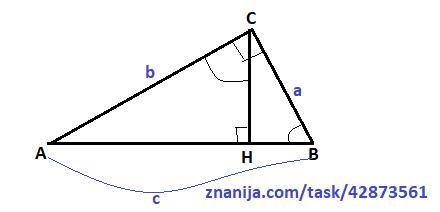
В прямоугольном ΔАВС, АВ=с, ВС=а, АС=в, СН⊥АВ, СН=h.Докажите, что а) h= ; в)
Объяснение:
а) ΔАВС подобен ΔАСН по двум углам :
∠АСВ=∠АНС=90° , ∠А-общий. В подобных треугольниках сходственные стороны пропорциональны ⇒ ,
, h=
;
в) Т.к " Катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу " , то
а= ⇒ a²=
(1);
b= ⇒ b²=
(2); Разделим первое уравнение на второе
или
или
.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: данил126
Предмет: Русский язык,
автор: 2классб
Предмет: Русский язык,
автор: natahaprokudin
Предмет: Математика,
автор: Кристина556882