Question

периметр правильного восьмиугольника вписанного в окружность равен 64 найдите периметр квадрата вписанного в ту же окружность ПОМОГИИТЕЕ ПОЖАЛУЙСТА, ДАЮ 44 БАЛЛА​

Answer 1

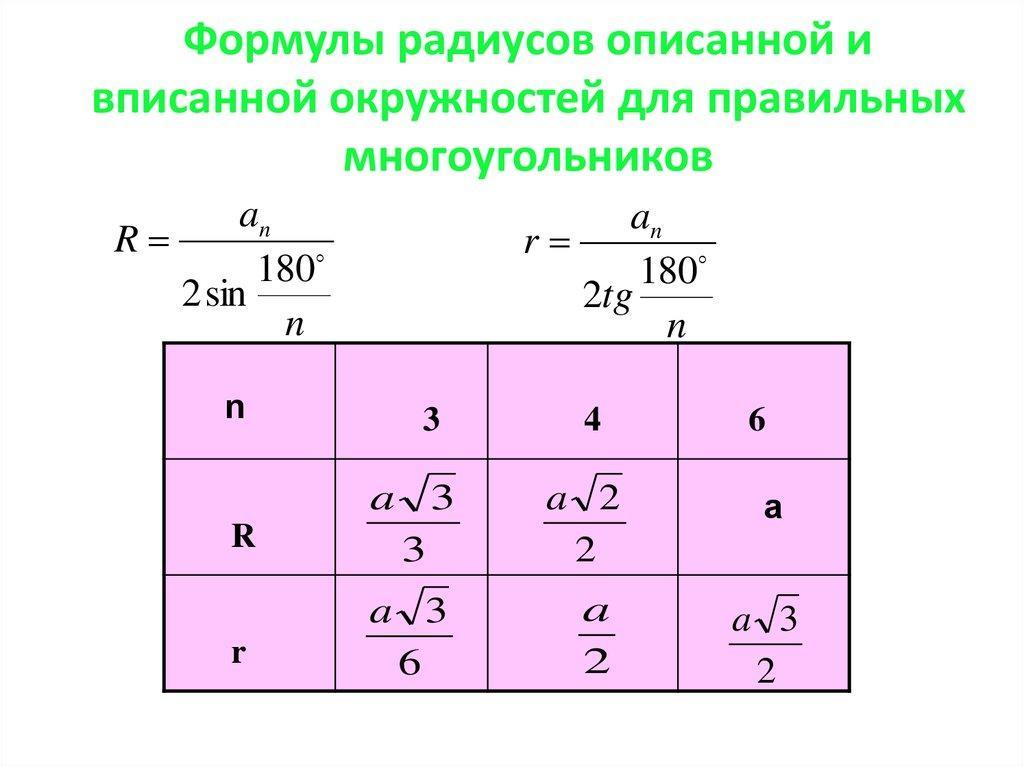
По формулам из фото определяем:

a₈=2Rsin(180°/8)

⇒  P₈/8=2Rsin(180°/8)

Выражаем радиус:

R=P₈/16sin22,5°

Через сторону квадрата: R=a√2/2

Т.к. это одна и та же окружность, радиусы приравниваем

P₈/16sin22,5° = a√2/2

a=2P₈/16√2sin22,5°

Если вы уже учили формулы подвоенного аргумента, то можем найти sin22,5°:

sin45°=2sin22,5°cos22,5°,     cos22,5°=√(1-sin²22,5°)

sin45°=2sin22,5°√(1-sin²22,5°)

√2/2=2sin22,5°√(1-sin²22,5°)  

(√2/2)² = (2sin22,5°√(1-sin²22,5°))²

2/4 = 4sin²22,5°(1-sin²22,5°)

1/2 =  4sin²22,5° - 4sin⁴22,5°

4sin²22,5° - 4sin⁴22,5°- 1/2 = 0

Замена: sin²22,5° = х, х>0

-4х² + 4х- 1/2 = 0

√D = √(16-4*4/2) = √(16-8) = √8 = 2√2

x₁ = (2√2-4) / -8 =   (2-√2) / 4

x₂  =   (-√2-2) / 4   (не подходит)

Обратная замена:  х = sin²22,5°

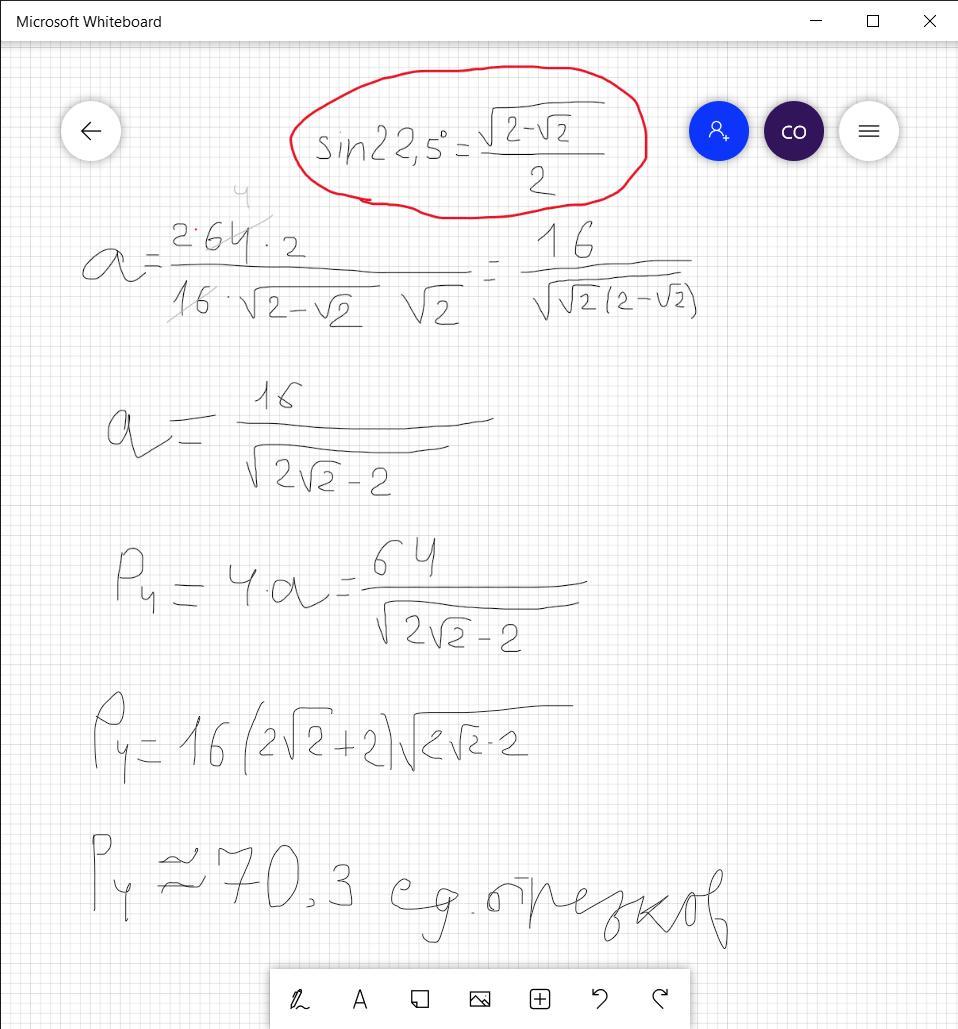
sin22,5°>0  ⇒  sin22,5° = √(2-√2) / 2 (на рисунке прикреплю, как это число выглядит)

Если же вы еще такого не учили, то просто смотрим на фото выведенный мною выше синус угла 22,5°

a=2P₈/16√2sin22,5°

Подставялем значения (тоже прикреплю фото для наглядности)

Ответ: 70,3 (приблизительно)

Честно, ответ какой-то подозрительно некрасивый, даже не знаю, почему