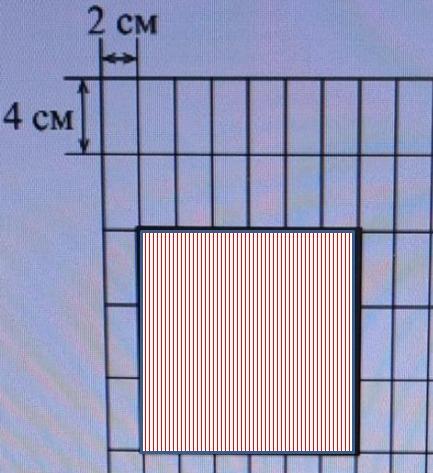
На рисунке дано поле, расчерченное на прямоугольники со сторонами 4 см и 2 см. На нём
изображена фигура.
1) Найдите площадь закрашенной фигуры. Ответ дайте в квадратных
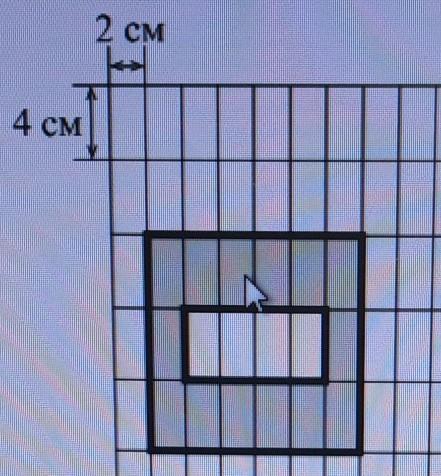
2) На поле, данном в условии, начертите прямоугольник, площадь которого равна 144 см.
Ответы
Ответ и Пошаговое объяснение:
Нужно знать:
а) 2-аксиома площади. Площадь фигуры, разбитой на несколько непересекающихся фигур, равна сумме площадей ее частей.
б) Площадь S прямоугольника со смежными сторонами a и b равна произведению этих сторон: S = a · b.
Решение.
1) Находим площадь S(4; 2) прямоугольника со смежными сторонами a=4 см и b=2 см:
S(4; 2) = 4·2 = 8 см².
Закрашенная фигура состоит из 14 прямоугольника со сторонами a=4 см и b=2 см. По 2-аксиоме:
S = 14·S(4; 2) = 14·8 = 112 см².
2) Нам нужно построить прямоугольник площадь которого равна 144 см². Определим число прямоугольников со сторонами a=4 см и b=2 см, из которых состоит прямоугольник с площадью равной 144 см²:
144 см² : 8 см² = 18.
Отсюда, если закрасить 18 клеток, то получим ответ для этой задачи (см. рисунок).