17. Диагональ прямоугольника образует угол
59° с одной из его сторон. Найдите острый угол
между диагоналями этого прямоугольника. От-
вет дайте в градусах.
Ответ:
Ответы
Ответ:
Острый угол между диагоналями прямоугольника равен 62°
Объяснение:
Известны свойства прямоугольника:
1) Все четыре угла прямоугольника прямые, то есть по 90°.
2) Диагонали прямоугольника равны, пересекаются и в точке пересечения делятся пополам, то есть образуются 4 равнобедренных треугольников.
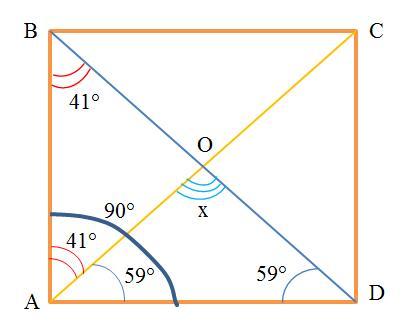
По условию один из углов между диагональю АС и стороной равен 59° (см. рисунок). Тогда другой угол диагональю АС и другой стороной равен 90°–59°=41°.
Известно, что сумма всех внутренних углов в треугольнике равна 180°. Так как
А) в равнобедренном треугольнике AOD углы при основании равны 59°, угол при вершине равен х = 180°–2∙59° = 62° < 90° - острый.
В) в равнобедренном треугольнике AOB углы при основании равны 41°, угол при вершине равен 180°–2∙41° = 98° > 90° - тупой.
Следовательно, искомый острый угол 62°.