Предмет: Алгебра,
автор: mowdy
Пользуясь правилами вычисления производных, найдите f' (x):
(см.фото)
Приложения:
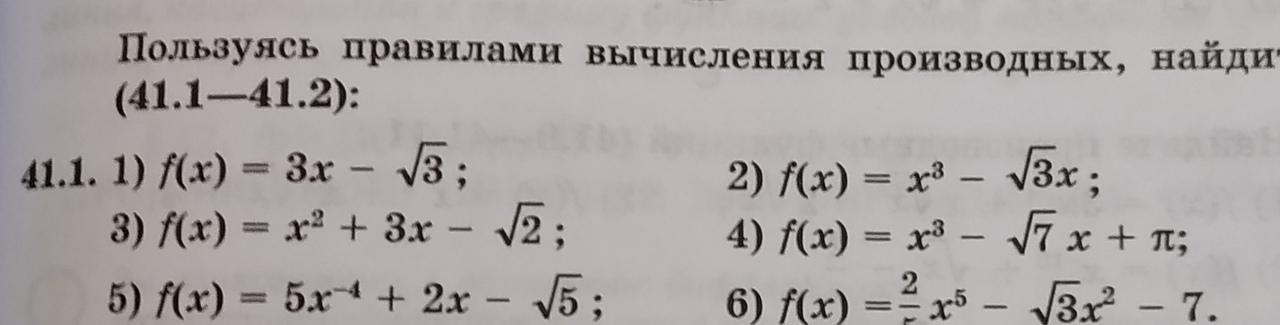
Ответы
Автор ответа:
23
Ответ:
1.
2.
3.
4.
5.
6.
Автор ответа:
11
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: g03041975
Предмет: Русский язык,
автор: aliya003
Предмет: Русский язык,
автор: hftyitt8
Предмет: Химия,
автор: Alina111alina
Предмет: Математика,
автор: drwnd