Question

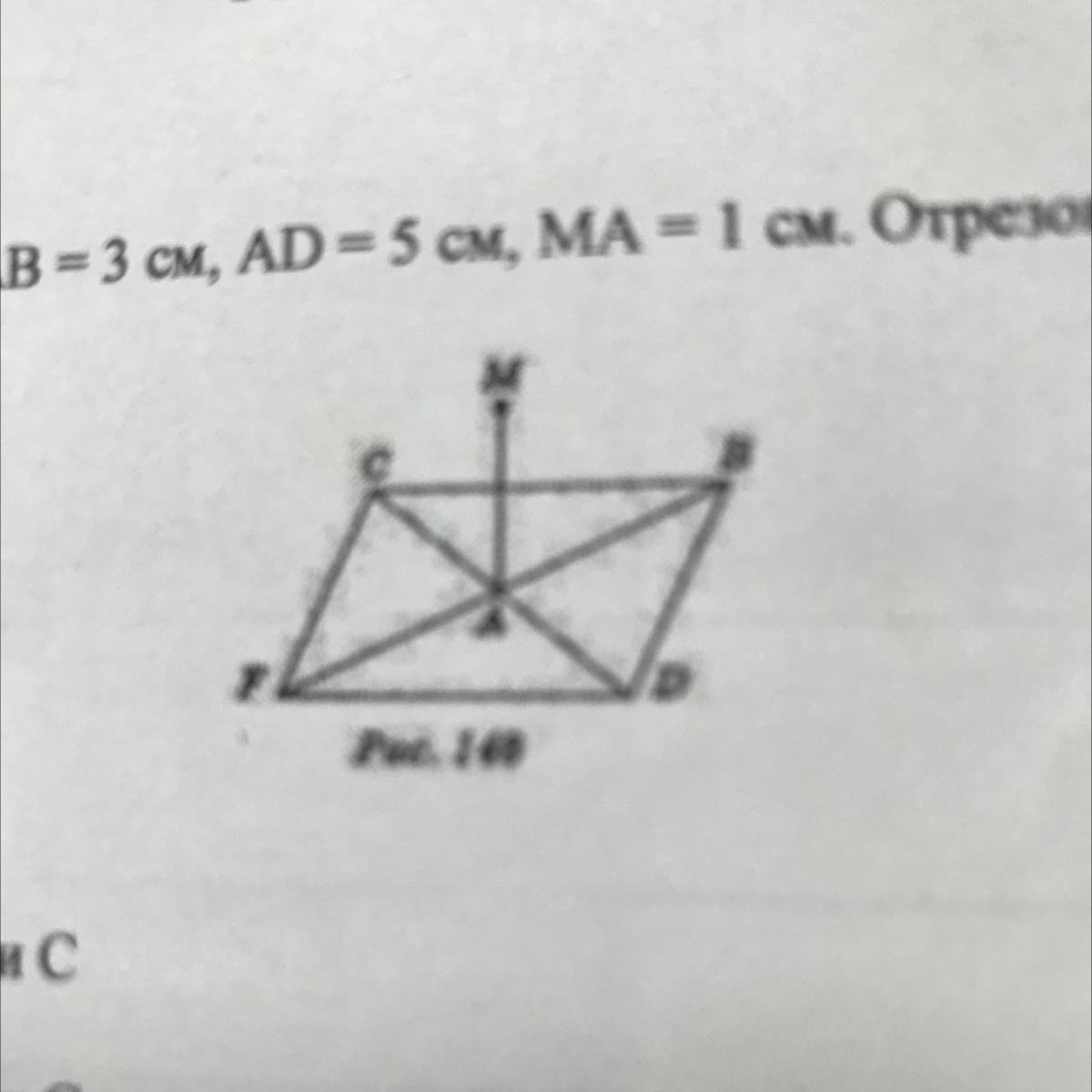
1. Дан ромб CBDF, в котором АВ = 3 см, AD =5 см, MA = 1 см. Отрезок MA перпендикулярен к
плоскости ABC.

Пользуясь рисунком, найдите:
1) расстояние между точками А и С
2) длину отрезка BD
3) расстояние между точками Мис
4) площадь треугольника MAC

Answer 1

Ответ:

1) Расстояние между точками А и С

Диагонали ромба в точке пересечения делятся пополам: АС=АD=5 см

2) длину отрезка BD

Диагонали ромба пересекаются под прямым углом (FB ⊥ СD). В прямоугольном треугольнике ABD по теореме Пифагора найдём гипотезу BD:

$BD = \sqrt{ {AB}^{2} + {AD}^{2} } = \sqrt{ {3}^{2} + {5}^{2} } = \sqrt{9 + 25} = \sqrt{36} = 6$

BD=6см

3) расстояние между точками М и С

Отрезок MA перпендикулярен к плоскости ABC. => МА перпендикулярен любой прямой в этой плоскости => МА⊥АС. Треугольник МАС- прямоугольный. По теореме Пифагора найдём гипотезу МС:

$MC = \sqrt{ {MA}^{2} + {AC}^{2} } = \sqrt{ {1}^{2} + {5}^{2} } = \sqrt{26}$ см

4) площадь треугольника MAC

Треугольник МАС- прямоугольный. площадь прямоугольного треугольника равна половине произведения его катетов:

$S = \dfrac{1}{2} AC \times MA = \dfrac{1}{2} \times 5 \times 1 = 2.5$ см²