Предмет: Геометрия,
автор: shahnoza19830216
В треугольнике АБС проведена медиана СД. Докажите, что угол АСД меньше угла ВСД, если АС>БС.
Ответы
Автор ответа:
6
Ответ:
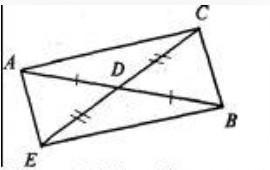
Продолжим медиану CD и отложим на ней отрезок DE = CD; полученный четырехугольник ACBЕ — параллелограмм. BE = AC и CB = AЕ.
В ΔACЕ ∠ACD лежит против стороны AЕ = CB. B ΔCBЕ ∠BCD лежит против стороны BE = AC. Так как AC > BC, то ∠ACD < ∠BCD. Что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: zasmin2003
Предмет: Русский язык,
автор: вася102
Предмет: Қазақ тiлi,
автор: KristaIdzumi
Предмет: Математика,
автор: Билли2017