Предмет: Математика,
автор: diastoleukhan
Найти интеграл, применив метод интегрирования по частям. Результат проверить дифференцированием.
(Даю хорошие баллы. Если можно, пожалуйста без лишнего. Найти интеграл, именно применив метод интегрирования по частям)

Приложения:
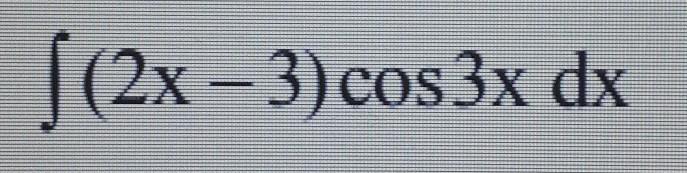
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Русский язык,
автор: nastyauvaeva
Предмет: Русский язык,
автор: yulia110
Предмет: Окружающий мир,
автор: dgylianna
Предмет: Математика,
автор: danyashherbakov