Предмет: Математика,
автор: diastoleukhan
Найти интеграл, результат проверить дифференцированием
(Даю хорошие баллы. Если можно, пожалуйста без лишнего)
![∫( \sin(x) + \frac{ {e}^{x} }{2} + \sqrt[6]{x} )dx ∫( \sin(x) + \frac{ {e}^{x} }{2} + \sqrt[6]{x} )dx](https://tex.z-dn.net/?f=%E2%88%AB%28+%5Csin%28x%29++%2B++%5Cfrac%7B+%7Be%7D%5E%7Bx%7D+%7D%7B2%7D++%2B++%5Csqrt%5B6%5D%7Bx%7D+%29dx)
Приложения:
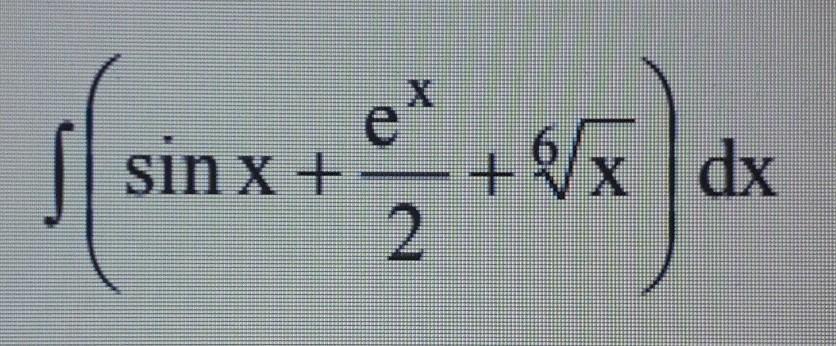
Ответы
Автор ответа:
2
Ответ:
diastoleukhan:
спасибо большое
Похожие вопросы
Предмет: Окружающий мир,
автор: verba84f
Предмет: Русский язык,
автор: nastyarodionov
Предмет: Русский язык,
автор: montiopo4ci
Предмет: Английский язык,
автор: Karolina9876