Предмет: Геометрия,
автор: Abcde1234554321
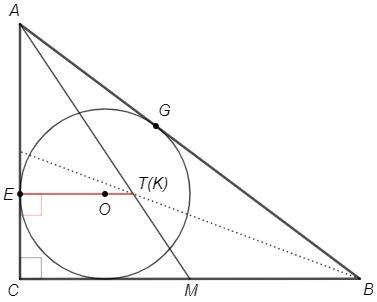
Помогите пожалуйста!!! Окружность с центром в точке О, вписанная в прямоугольный треугольник Abc касается катетов AC и Вс в точках Е и D соответственно, гипотенузы Ав - в точке G. Известно, что CE =3 AG = 6
Докажите, что прямая Ое проходит через точку К пересечения медиан треугольника АВС.
Ответы
Автор ответа:
4
AE=AG =6 (отрезки касательных из одной точки)
OE⊥AC (радиус в точку касания) => OE||BC
Пусть OE пересекает медиану AM в точке T.
AT/TM =AE/EC =6/3 =2/1 (т. о пропорциональных отрезках)
AK/KM =2/1 (медианы точкой пересечения делятся 2:1 от вершины)
Следовательно точки T и K совпадают, то есть OE проходит через точку пересечения медиан.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: монти1
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: Аноним
Предмет: Українська література,
автор: anastasia576654