Предмет: Математика,
автор: vidergunova503
40 баллов . Упростите выражение:
срочнооо
Приложения:
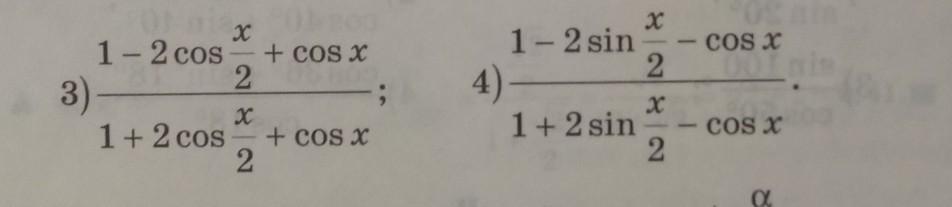
Ответы
Автор ответа:
3
Ответ:
3
4
25hjoerf10:
Добрый вечер, Miroslava! Мне очень нужна помощь по теории вероятности. Пожалуйста, посмотрите задание в моем профиле. Одна задача на 100 баллов. Буду очень благодарна за помощь!
Похожие вопросы
Предмет: Українська мова,
автор: Lenzze
Предмет: Английский язык,
автор: krutnoc
Предмет: Русский язык,
автор: waniafff
Предмет: Физика,
автор: уфф4
Предмет: История,
автор: tawer2283377