Предмет: Алгебра,
автор: Лера250
Решите неравенства: 1) 6x+1//3+x>0 ; 2) 5x//4x-12<0. Найдите множество решений неравенства: 1) 2-x//x больше или равно 0; 2) 3-2x//x-1 меньше или равно 0.
Ответы
Автор ответа:
0
1) 
Решим линейное уравнение 6x+1=0
Корень уравнения: x=−1/6
теперь линейное уравнение x+3=0
Корень уравнения: x=−3
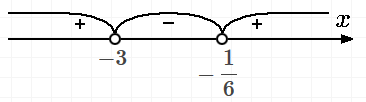
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале. (см. приложение)
Ответ: x∈(−∞;−3)∪(−16;+∞)
или

2)
Корни уравнения 5x=0
x1=0
линейное уравнение x−12=0
Корень уравнения: x=12
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
Ответ: x∈(0;12) или 0<x<12
3)
линейное уравнение −x+2=0
Корень уравнения: x=2
линейное уравнение x=0
Корень линейного уравнения: x=0
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
Ответ: x∈(0;2] или 0<x≤2
4)
Решим линейное уравнение −2x+3=0
Корень уравнения: x=1,5
Решим линейное уравнение x−1=0
Корень уравнения: x=1
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
Ответ: x∈(−∞;1)∪[1,5;+∞) или x<1;x≥1,5
Решим линейное уравнение 6x+1=0
Корень уравнения: x=−1/6
теперь линейное уравнение x+3=0
Корень уравнения: x=−3
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале. (см. приложение)
Ответ: x∈(−∞;−3)∪(−16;+∞)
или
2)
Корни уравнения 5x=0
x1=0
линейное уравнение x−12=0
Корень уравнения: x=12
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
Ответ: x∈(0;12) или 0<x<12
3)
линейное уравнение −x+2=0
Корень уравнения: x=2
линейное уравнение x=0
Корень линейного уравнения: x=0
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
Ответ: x∈(0;2] или 0<x≤2
4)
Решим линейное уравнение −2x+3=0
Корень уравнения: x=1,5
Решим линейное уравнение x−1=0
Корень уравнения: x=1
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
Ответ: x∈(−∞;1)∪[1,5;+∞) или x<1;x≥1,5
Приложения:



Автор ответа:
0
Спасибо большое))) только вот я не поняла во втором уравнении как получилось x1 =0?
Автор ответа:
0
5*x = 0 - это верно только при х =0
Автор ответа:
0
Решите неравенства:
Здесь везде используем метод интервалов для этого ищем точки перехода, когда знаменатель и числитель равняются 0 и применяем метод интервалов
1) (6x+1)/(3+x)>0 ;
===============-3==========-1/6===========
+++++++++++++++ ------------------- ++++++++
(-,бесконечность -3) U (-1/6 ,+ бесконечность)
2) 5x/(4x-12)<0.
===============0==============3==============
++++++++++++++ ----------------------- +++++++++++++
(0 3)
Найдите множество решений неравенства:
1) (2-x)/x >= 0
================0=============2===========
--------------------------++++++++++++++ -------------------
(0 2]
; 2) (3-2x)/(x-1) <= 0
===========1=========3/2===========
------------------- ++++++++++ ----------------
(-бесконечность 1) U [3/2 +бесконесность)
=====================
скобки )( не включают решение
][ включают.
Здесь везде используем метод интервалов для этого ищем точки перехода, когда знаменатель и числитель равняются 0 и применяем метод интервалов
1) (6x+1)/(3+x)>0 ;
===============-3==========-1/6===========
+++++++++++++++ ------------------- ++++++++
(-,бесконечность -3) U (-1/6 ,+ бесконечность)
2) 5x/(4x-12)<0.
===============0==============3==============
++++++++++++++ ----------------------- +++++++++++++
(0 3)
Найдите множество решений неравенства:
1) (2-x)/x >= 0
================0=============2===========
--------------------------++++++++++++++ -------------------
(0 2]
; 2) (3-2x)/(x-1) <= 0
===========1=========3/2===========
------------------- ++++++++++ ----------------
(-бесконечность 1) U [3/2 +бесконесность)
=====================
скобки )( не включают решение
][ включают.
Приложения:




Похожие вопросы
Предмет: Биология,
автор: masyan2008
Предмет: Английский язык,
автор: patrakova09
Предмет: Қазақ тiлi,
автор: svobodno90
Предмет: Геометрия,
автор: annets21
Предмет: Химия,
автор: NastyaBernik