Question

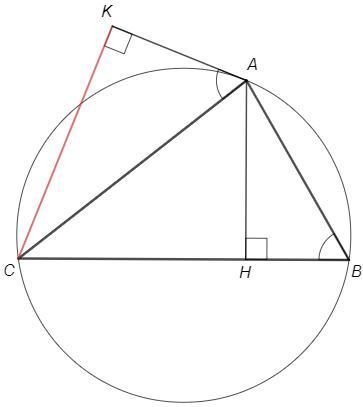
Треугольник `ABC` со сторонами `AB=5`, `BC=8`, `AC=7` вписан в окружность. Найти расстояние от точки `C` до касательной к окружности, проходящей через точку `A`.

Answer 1

Угол между касательной и хордой равен половине дуги, стягиваемой хордой.

∠CAK =∪AC/2 =∠B

△ABC, теорема косинусов

cosB = (AB^2 +CB^2 -CA^2)/2AB*CB = (25+64-49)/2*5*8 =1/2

sinCAK =sinB =√(1-cosB^2) =√3/2

(синус угла треугольника положительный)

CK =AC*sinCAK =7√3/2

Или

△ABC, формула Герона

p =(5+8+7)/2 =10

S =√(10*5*2*3) =10√3

S =1/2 BC*AH => AH=5√3/2

△CAK~△ABH => CK/AH =AC/AB =7/5 => CK=7√3/2