Question

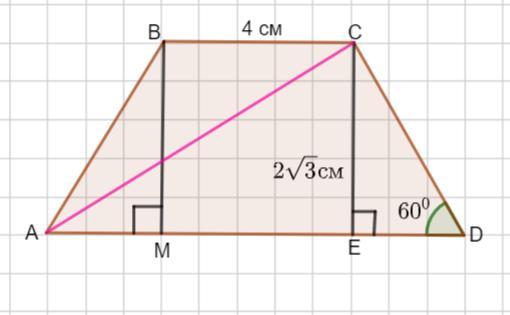
У рівнобічній трапеції ABCD основа ВС = 4см, висота СЕ = 2√3см, а бічна сторона утворює з основою AD кут 60⁰. Знайдіть діагональ трапеції

​

Answer 1

Ответ:

$4\sqrt{3}$ см.

Объяснение:

Пусть задана равнобедренная трапеция ABCD.

ВС= 4см, высота СЕ= 2√3 см,  ∠ А= ∠D=60 °.

Так как СЕ - высота, то треугольник Δ СЕD - прямоугольный.

Тангенсом острого угла прямоугольного треугольника называется  отношение противолежащего катета к прилежащему.

$tg 60^{0} =\dfrac{CE}{ED } ;\\\\ED= \dfrac{CE }{tg 60^{0}} ;\\\\ED= \dfrac{2\sqrt{3} }{tg 60^{0}} = \dfrac{2\sqrt{3} }{\sqrt{3} } = 2$

Если в равнобедренной трапеции провести еще высоту ВМ, то АМ = ЕD= 2 см.

Найдем длину отрезка АЕ

АЕ = АМ +МЕ ;

АЕ = 2+4 =6 см.

Рассмотрим Δ  АСЕ - прямоугольный и найдем АС по теореме Пифагора : в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AC ^{2} = CE^{2} + AE ^{2} ;\\ AC= \sqrt{ CE^{2} + AE ^{2}} ;\\AC= \sqrt{(2\sqrt{3})^{2} +6^{2} } =\sqrt{12+36} =\sqrt{48} =\sqrt{16\cdot3 } =4\sqrt{3}$

Значит, диагональ АС =4√3 см. У равнобедренной трапеции диагонали равны. Тогда  $BD=AC= 4\sqrt{3}$  см.