Предмет: Алгебра,
автор: Alexandr5678
Избавьтесь от иррациональности в знаменателе дроби:
Приложения:
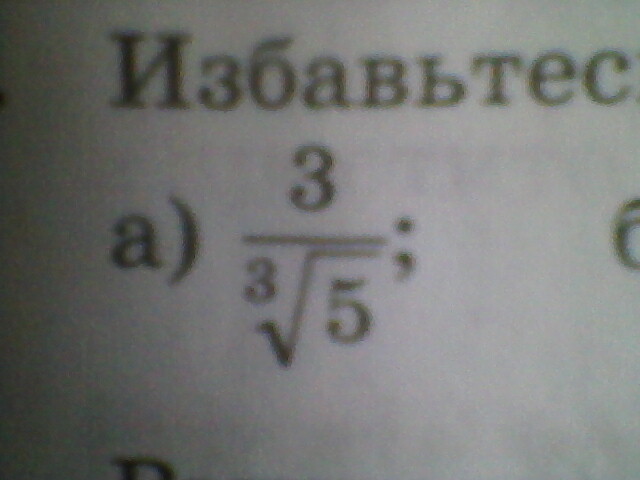
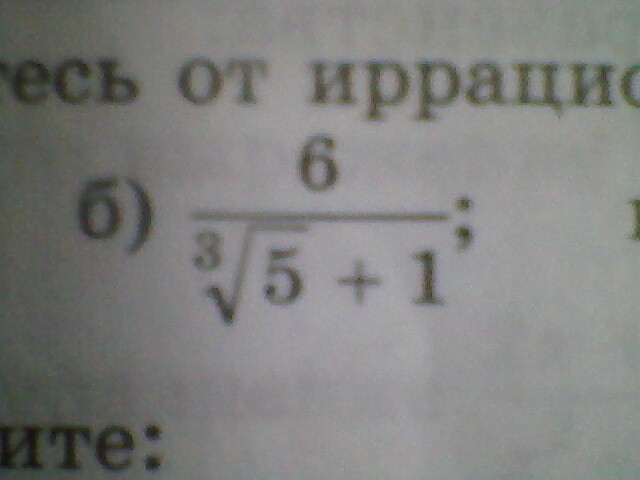
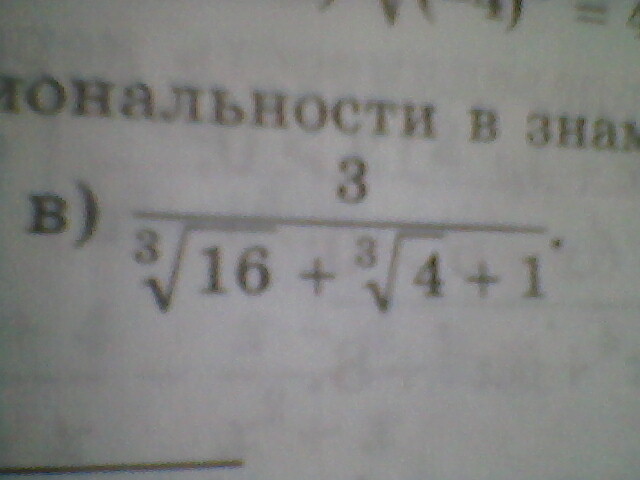
Ответы
Автор ответа:
0
1) ![frac{3}{ sqrt[3]{5} }= frac{3}{ sqrt[3]{5} } *1= frac{3}{ sqrt[3]{5} }* frac{ sqrt[3]{5^2} }{ sqrt[3]{5^2} } = frac{3 sqrt[3]{5^2} }{ sqrt[3]{5^3} } = frac{ 3sqrt[3]{5^2} }{5} frac{3}{ sqrt[3]{5} }= frac{3}{ sqrt[3]{5} } *1= frac{3}{ sqrt[3]{5} }* frac{ sqrt[3]{5^2} }{ sqrt[3]{5^2} } = frac{3 sqrt[3]{5^2} }{ sqrt[3]{5^3} } = frac{ 3sqrt[3]{5^2} }{5}](https://tex.z-dn.net/?f=+frac%7B3%7D%7B+sqrt%5B3%5D%7B5%7D+%7D%3D+frac%7B3%7D%7B+sqrt%5B3%5D%7B5%7D+%7D+%2A1%3D+frac%7B3%7D%7B+sqrt%5B3%5D%7B5%7D+%7D%2A+frac%7B+sqrt%5B3%5D%7B5%5E2%7D+%7D%7B+sqrt%5B3%5D%7B5%5E2%7D+%7D+%3D+frac%7B3+sqrt%5B3%5D%7B5%5E2%7D+%7D%7B+sqrt%5B3%5D%7B5%5E3%7D+%7D+%3D+frac%7B+3sqrt%5B3%5D%7B5%5E2%7D+%7D%7B5%7D+)
2)![frac{6}{ sqrt[3]{5}+1 } = frac{6}{ sqrt[3]{5}+1 }* frac{ sqrt[3]{5^2}- sqrt[3]{5}+1}{ sqrt[3]{5^2}- sqrt[3]{5}+1} = frac{6( sqrt[3]{5^2}- sqrt[3]{5}+1)}{ (sqrt[3]{5})^3+1^3 } = sqrt[3]{5^2}- sqrt[3]{5}+1 frac{6}{ sqrt[3]{5}+1 } = frac{6}{ sqrt[3]{5}+1 }* frac{ sqrt[3]{5^2}- sqrt[3]{5}+1}{ sqrt[3]{5^2}- sqrt[3]{5}+1} = frac{6( sqrt[3]{5^2}- sqrt[3]{5}+1)}{ (sqrt[3]{5})^3+1^3 } = sqrt[3]{5^2}- sqrt[3]{5}+1](https://tex.z-dn.net/?f=+frac%7B6%7D%7B+sqrt%5B3%5D%7B5%7D%2B1+%7D+%3D+frac%7B6%7D%7B+sqrt%5B3%5D%7B5%7D%2B1+%7D%2A+frac%7B+sqrt%5B3%5D%7B5%5E2%7D-+sqrt%5B3%5D%7B5%7D%2B1%7D%7B+sqrt%5B3%5D%7B5%5E2%7D-+sqrt%5B3%5D%7B5%7D%2B1%7D+%3D+frac%7B6%28+sqrt%5B3%5D%7B5%5E2%7D-+sqrt%5B3%5D%7B5%7D%2B1%29%7D%7B+%28sqrt%5B3%5D%7B5%7D%29%5E3%2B1%5E3+%7D+%3D+sqrt%5B3%5D%7B5%5E2%7D-+sqrt%5B3%5D%7B5%7D%2B1)
3)![frac{3}{ sqrt[3]{4^2} + sqrt[3]{4}+1 } = frac{3}{ sqrt[3]{4^2} + sqrt[3]{4}+1 }* frac{ sqrt[3]{4} -1}{sqrt[3]{4} -1} = sqrt[3]{4} -1 frac{3}{ sqrt[3]{4^2} + sqrt[3]{4}+1 } = frac{3}{ sqrt[3]{4^2} + sqrt[3]{4}+1 }* frac{ sqrt[3]{4} -1}{sqrt[3]{4} -1} = sqrt[3]{4} -1](https://tex.z-dn.net/?f=+frac%7B3%7D%7B+sqrt%5B3%5D%7B4%5E2%7D+%2B+sqrt%5B3%5D%7B4%7D%2B1+%7D+%3D+frac%7B3%7D%7B+sqrt%5B3%5D%7B4%5E2%7D+%2B+sqrt%5B3%5D%7B4%7D%2B1+%7D%2A+frac%7B+sqrt%5B3%5D%7B4%7D+-1%7D%7Bsqrt%5B3%5D%7B4%7D+-1%7D+%3D+sqrt%5B3%5D%7B4%7D+-1)
В первом случае: просто дополнил корень до нужной степени.
Второй случай: формула
Третий случай: формула
Внимание на знаки в формулах!
Обобщение разности n степеней: (бином Ньютона).
(бином Ньютона).
2)
3)
В первом случае: просто дополнил корень до нужной степени.
Второй случай: формула
Третий случай: формула
Внимание на знаки в формулах!
Обобщение разности n степеней:
Похожие вопросы
Предмет: Математика,
автор: yfyfufufufufufufu
Предмет: МХК,
автор: lizua572882
Предмет: Қазақ тiлi,
автор: zepetohaus141
Предмет: Химия,
автор: TheHost
Предмет: Алгебра,
автор: iSLim