Предмет: Математика,
автор: tatyhdifh020
100 раз прошу уже. Упростите выражение:
Приложения:
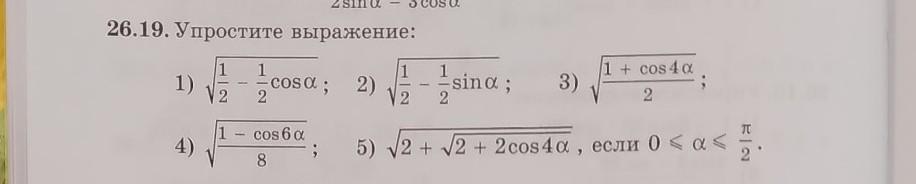
Ответы
Автор ответа:
1
tatyhdifh020:
Здравствуйте
Можете помочь это такое задание почти
Тригонометрия
Преобразуйте выражение в произведение:
https://znanija.com/task/42913172?utm_source=android&utm_medium=share&utm_campaign=question
https://znanija.com/task/42913172?utm_source=android&utm_medium=share&utm_campaign=question
Пожалуйста пожалуйста
Похожие вопросы
Предмет: Русский язык,
автор: cdhb
Предмет: Русский язык,
автор: jkzzhbyf
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: lera2003053012
Предмет: Алгебра,
автор: Morgandi321