Предмет: Геометрия,
автор: jejsmsmkskekdnsn
Знатоки геометрии, хелп!
Прямоугольный треугольник ABC(уголC=90°). Катет АС соприкасается с окружностью в точке D, а катет BC пересекает ту же окружностью. Центр окружности O находиться на гипотенузе AB. Найдите длину радиуса окружности если AC=4см, BC=3см.
(Можно с рисунком, пожалуйста)
68tata:
Это перевод задачи на русский язык? можно фото задания?
да, это перевод
слово в слово перевел
условие неполное
попробую перефразировать
Катет АС прямоугольного треугольника ABC(уголC=90°) касается окружности(круга) в точке D, а катет BC пересекает эту окружность(круг). Центр окружности O находиться на гипотенузе AB. Найдите длину окружности радиуса если AC=4см, BC=3см.
с какого языка? , если с украинского дай фото, Не понятно : а катет BC пересекает ту же окружностью.
не с украинского
"Катет BС пересекает эту окружность"
Ответы
Автор ответа:
1
Ответ: 2,5 см
Решение:
Это свойство прямоугольного треугольника, вписанного в окружность!!!!
Центр такой окружности лежит на гипотенузе , причём делит её пополам
Так как у тебя задан классический египетский треугольник с катетами 3см и 4см, то его гипотенуза равна 5 см( или реши по теореме Пифагора:
АВ²= ВС²+АС²=3²+4²=25 (см²)
АВ=√25=5 (см)
R= AB:2=5:2=2,5 (см)
Приложения:
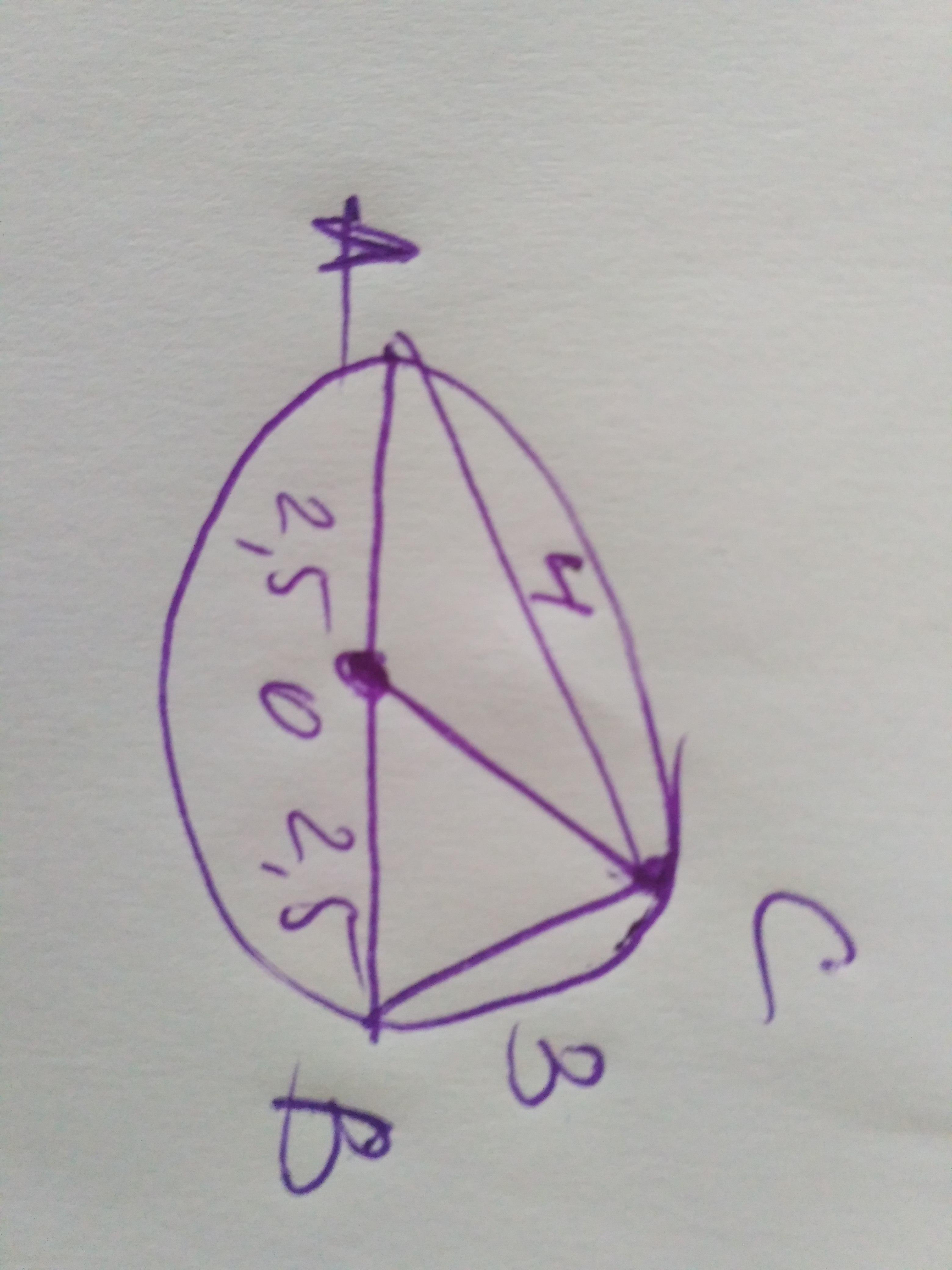
Похожие вопросы
Предмет: Русский язык,
автор: ксюша510
Предмет: Русский язык,
автор: kurbakovalina
Предмет: Русский язык,
автор: maydatd
Предмет: Английский язык,
автор: ДаниилСотников
Предмет: Математика,
автор: viktoriavioka1