Предмет: Алгебра,
автор: volodyayaremyn
Вирішити рівняння з логорифмом:
Приложения:
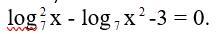
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ: х>0
- логарифмическое квадратное уравнение, замена переменной,
обратная замена:
Автор ответа:
1
log²(7) x - log(7) x² - 3 = 0
x > 0
log²(7) x - 2*log(7) x - 3 = 0
log(7) x = t
t² - 2t - 3 = 0
D = 4 + 12 = 16
t12 = (2 +- 4)/2 = -1 3
1. t1 = 3
log(7) x = 3
x = 7³ = 343
2. t2 = -1
log(7) x = -1
x = 1/7
ответ х = {1/7, 343}
Похожие вопросы
Предмет: Английский язык,
автор: natalyapom43
Предмет: Английский язык,
автор: va5241
Предмет: Русский язык,
автор: Munya1
Предмет: Химия,
автор: misisx07
Предмет: Алгебра,
автор: nargiznaraali