Question

Один из острых углов прямоугольного треугольника равен 60°, а сумма меньшего катета и гипотенузы равна 42 см.
Определи длину меньшего катета.

1. Величина второго острого угла равна
°.
2. Длина меньшего катета равна
см.

Answer 1

Ответ:

∠BAC = 30°

BC = 14 см

Объяснение:

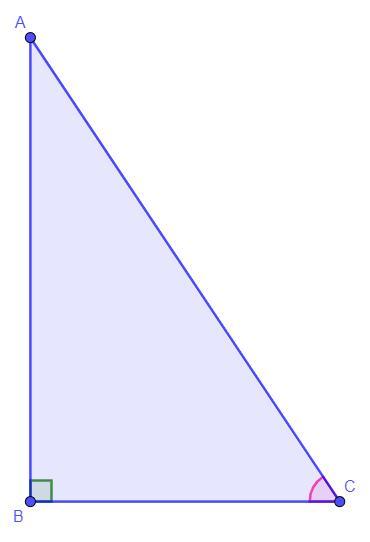
Дано: ∠ABC = 90°, BC + AC = 42 см, ∠BCA = 60°

Найти: ∠BAC, BC - ?

Решение:

По теореме про сумму углов треугольника для треугольника ΔABC:

∠BCA + ∠ABC + ∠BAC = 180° ⇒ ∠BAC = 180° - ∠BCA - ∠ABC =

= 180° - 60° - 90° = 90° - 60° = 30°.

Так как угол ∠BCA в треугольнике наименьший, то по теореме против наименьшего угла лежит наименьшая сторона.

Так как по условию треугольник ΔABC прямоугольный, то определению косинуса в прямоугольном треугольнике (∠ABC = 90°):

$\cos \angle BCA = \dfrac{BC}{AC} \Longrightarrow BC = AC \cdot \cos \angle BCA = AC \cdot \cos 60^{\circ} = 0,5AC$.

BC + AC = 42

0,5AC + AC = 42

1,5AC = 42|:1,5

AC = 28 см.

BC = 0,5AC = 0,5 * 28 = 14 см.