Предмет: Математика,
автор: bozenko02
Помогите решить пожалуйста Срочно
Приложения:
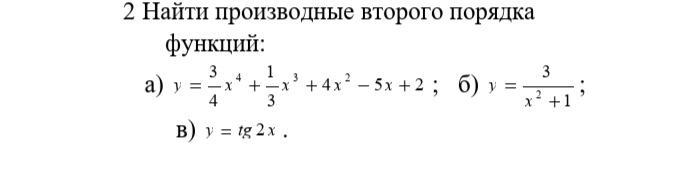
Ответы
Автор ответа:
2
Ответ:
a
б
в
Похожие вопросы
Предмет: Русский язык,
автор: 8207
Предмет: Окружающий мир,
автор: sidevytov19821
Предмет: Русский язык,
автор: micic04
Предмет: Физика,
автор: anujtik2003
Предмет: Физика,
автор: aiskx