Предмет: Алгебра,
автор: bapataidamir2004
ЛОГАРИФМ! ПОМОГИТЕ ПОЖАЛУЙСТА!
Приложения:
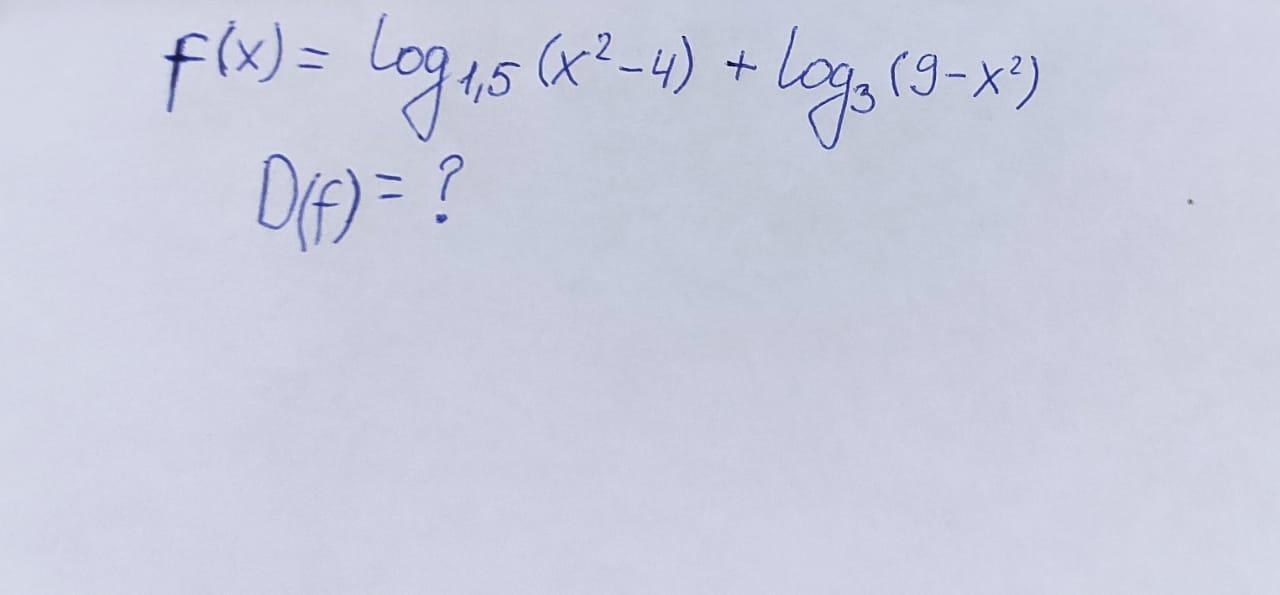
Ответы
Автор ответа:
1
Объяснение:
ОДЗ:
(x+2)(x-2)>0
-∞__+__-2__-__2__+__+∞
x∈(-∞;-2)U(2;+∞).
(x+3)(x-3)<0
-∞__+__-3__-__3__+__+∞
x∈(-3;3). ⇒
Ответ: x∈(-3;-2)U(2;3).
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: bezvinnaya84
Предмет: Қазақ тiлi,
автор: Дикошаа
Предмет: Французский язык,
автор: МарияНяша
Предмет: Математика,
автор: zykovaalina54555
Предмет: Математика,
автор: murat8998