Предмет: Геометрия,
автор: jasmin9115
помогите пожалуйста срочно надо
Приложения:

Ответы
Автор ответа:
1
Обозначим длину биссектрисы СД и отрезок АД стороны АВ за "х".
При равенстве АД и СД точка Д находится на перпендикуляре к середине стороны АС, точка Д1 - это проекция Д на АС.
Значит, АД1 = 7/2 = 3,5.
Воспользуемся свойством биссектрисы: АД : ДВ = 7 : 9.
Поэтому ДВ = (9/7)х, а сторона АВ = х + (9/7)х = (16/7)х.
Тогда отрезок АВ1 (В1 - это проекция точки В на АС ) равен (16/7)*(7/2) = 8.
То есть, проекция АВ на АС длиннее АС на 8 - 7 = 1.
Тогда высота точки В равна √(9² - 1²) = √80.
Находим длину стороны АВ, по Пифагору: АВ = √(64 + 80) = √144 = 12.
Теперь можно определить АД = СД из условия:
(16/7)х = 12, отсюда х = 12*7/16 = 21/4.
Ответ: СД = 21/4.
marinkal68:
мне помогите пожалуйста
Автор ответа:
1
Ответ: 3 варианта решения
Объяснение:
Приложения:
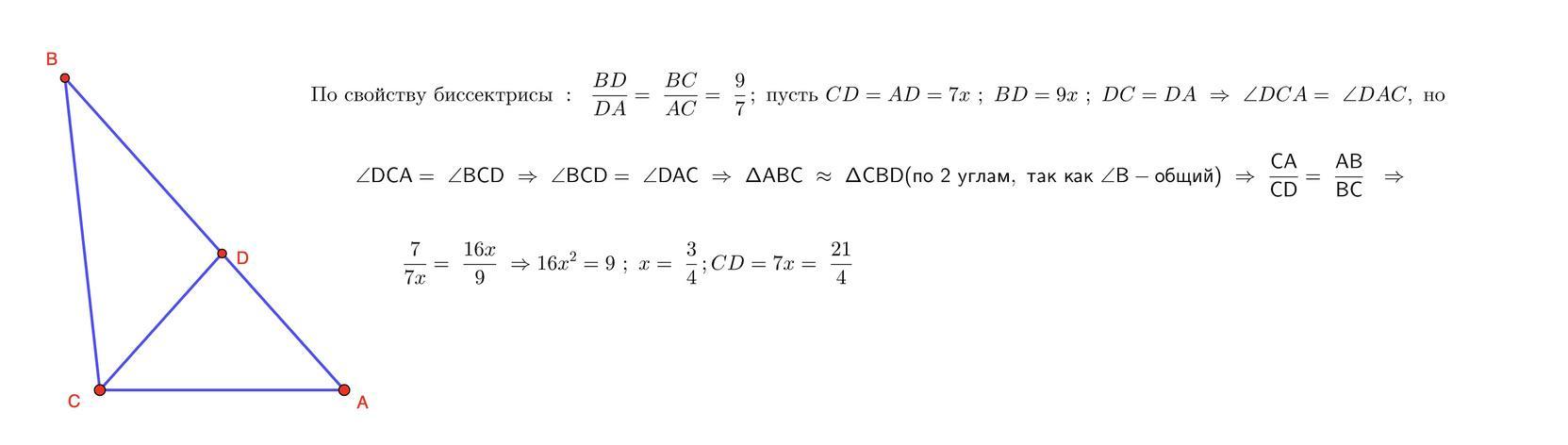
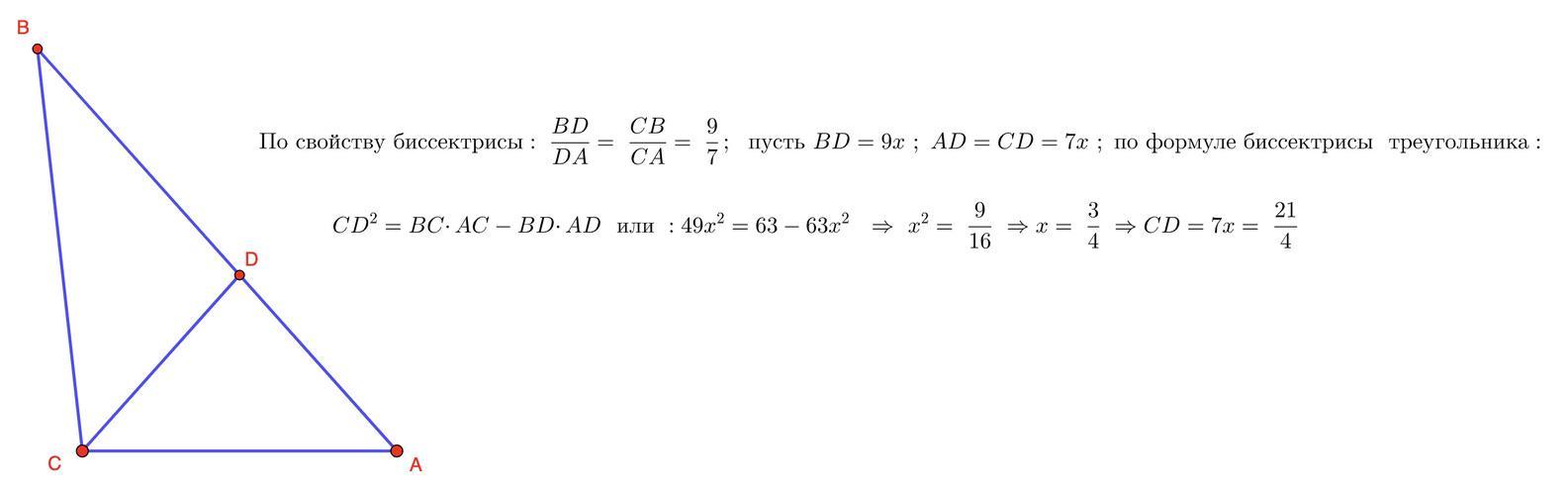

Похожие вопросы
Предмет: Русский язык,
автор: nokiz
Предмет: Українська мова,
автор: 190665
Предмет: Русский язык,
автор: shishlova751
Предмет: Математика,
автор: votin4is
Предмет: История,
автор: lleo232629p4l5mr