Question

Один из острых углов прямоугольного треугольника равен 60°, а сумма меньшего катета и гипотенузы равна 12 см.
Определи длину меньшего катета.

1. Величина второго острого угла равна
°.
2. Длина меньшего катета равна
см.

Answer 1

Нужно знать:

1. Сумма острых углов прямоугольного треугольника равна 90°.

2. Против большей стороны лежит больший угол, против меньшей стороны  - меньший угол.

3. Катет, лежащий против угла в 30°, равен половине гипотенузы.

Поэтому:

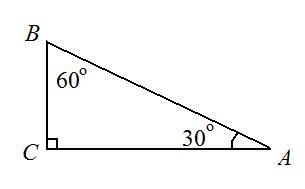
пусть дан прямоугольный ΔАВС (см. рис.), ∠В = 60°, ВС + АВ = 12 см. Найдем ВС.

Т.к. ∠В + ∠А = 90°, то ∠А = 90° - 60° = 30°.

Следовательно, катет ВС лежит против угла в 30° - меньший катет.

Тогда т.к. АВ = 2ВС и ВС + АВ = ВС + 2ВС = 3ВС = 12 см, откуда

ВС = 4 см.

Ответ: 4 см.