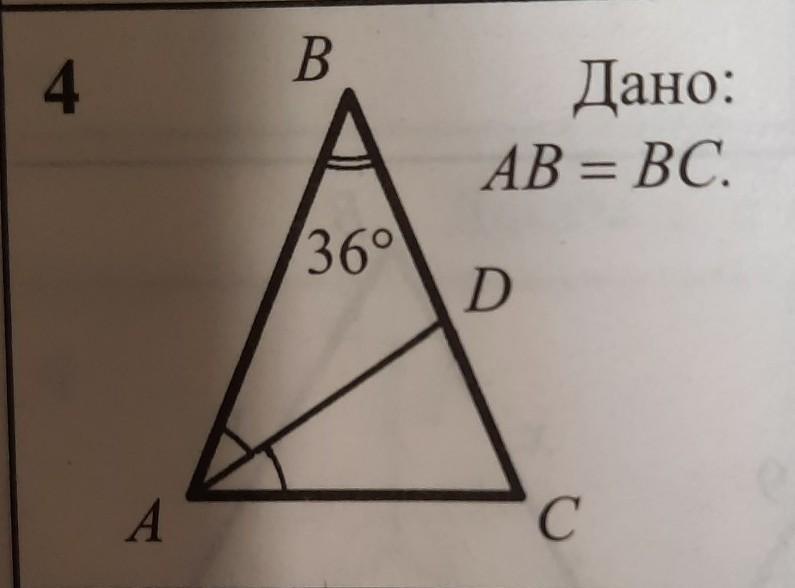
Помогите пожалуйста!!!
Указать подобные треугольники, доказать их подобие.
Ответы
Ответ:
Треугольник abd подобен adc.
Объяснение: 1. Угол b равен углу DAC т.к это р/б треугольник и можно найти углы A и C (180-36=144, делим на 2 так как углы равны, равняется 72). AD- биссектриса и делит угл A на 2 (72/2=36, значит BAD и DAC=36)
2. Угол C равен углу BDA так как треугольник BAD - р/б. Так как угл BAD=36 и ABD=36 можно найти BDA (180-36-36=72), а угл C=72 по первому пункту (так как угл A равен углу C как р/б треугольник).
Получается что Угол B=DAC и угол C=BDA
Значит подобны по первому признаку по двум углам
Ответ:
Треугольники ABC и ADC подобны.
Объяснение:
1) Т.к. треугольник ABC равнобедренный, следовательно углы BAC и BCA = (180-36)/2 = 72 градуса
2) AD - биссектриса угла BAC, что видно из чертежа, следовательно углы BAD и DAC равны по 36 градусов.
Собираем картинку:
угол DAC = углу ABD = 36 градусов
угол BAC = углу BCA = 72 градуса
следовательно треугольники ABC и ADC подобны по первому признаку (по 2 углам)