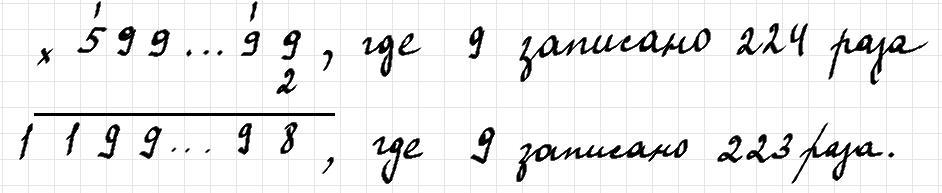Question

омогите пожалуйста срочно !!! n-наименьшее натуральное число сумма цифр которого равна 2021
1 найти число n

2 найдите сумму цифр числа 2n

Answer 1

Ответ:

а) $n=5*10^{225}+9*10^{224}+9*10^(223)+...+9*10+9$

б) 2017

Пошаговое объяснение:

Нужно найти наименьшее натуральное число, значит количество разрядов в нем должно быть наименьшим. Значит в записи числа должно быть использовано как можно больше девяток.

2021 не кратно 9, значит сумму цифр искомого числа можно представить в виде выражения

9а + х, где а - число девяток в записи исходного числа, х - однозначное натуральное число.

До 2021 самое большое число, кратное 9 это 2016, т.е. сумма цифр исходного числа будет выглядеть так: 9а + 5, где 9а = 2016.

а=2016:9=224.

В записи исходного натурального числа использовано 224 девятки и одна пятерка. Цифру 5 поставим на первое место, тогда число будет наименьшим.

В виде суммы разрядных слагаемых число выглядит так:

$n=5*10^{225}+9*10^{224}+9*10^{223}+...+9*10+9$

Тогда число 2n в виде суммы разрядных слагаемых будет выглядеть так:

$2n=1*10^{226}+1*10^{225}+9*10^{224}+9*10^{223}+...+9*10+8$

(умножение в столбик см. на фото).

Сумма цифр числа 2n будет равна

$223*9+8+1+1=2017$