Предмет: Математика,
автор: hopiluka
Найти пределы функций

professional65:
нифига это не математика!
Это алгебра!
Ответы
Автор ответа:
1
......................................
Приложения:
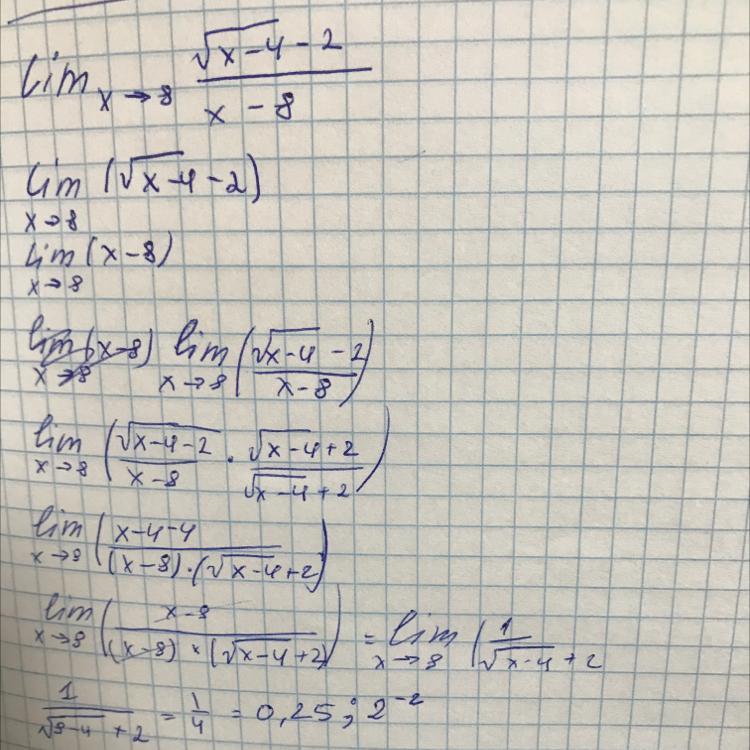
Автор ответа:
0
Ответ:
=0,25
Пошаговое объяснение:
неопределенность вида 0/0
Похожие вопросы
Предмет: Английский язык,
автор: NataliaVolovich1
Предмет: Английский язык,
автор: Irinaladushkin
Предмет: Русский язык,
автор: gemu14
Предмет: Другие предметы,
автор: DanyGuy