задачка по геометрии помогите
Ответы
Відповідь:
8
Пояснення:
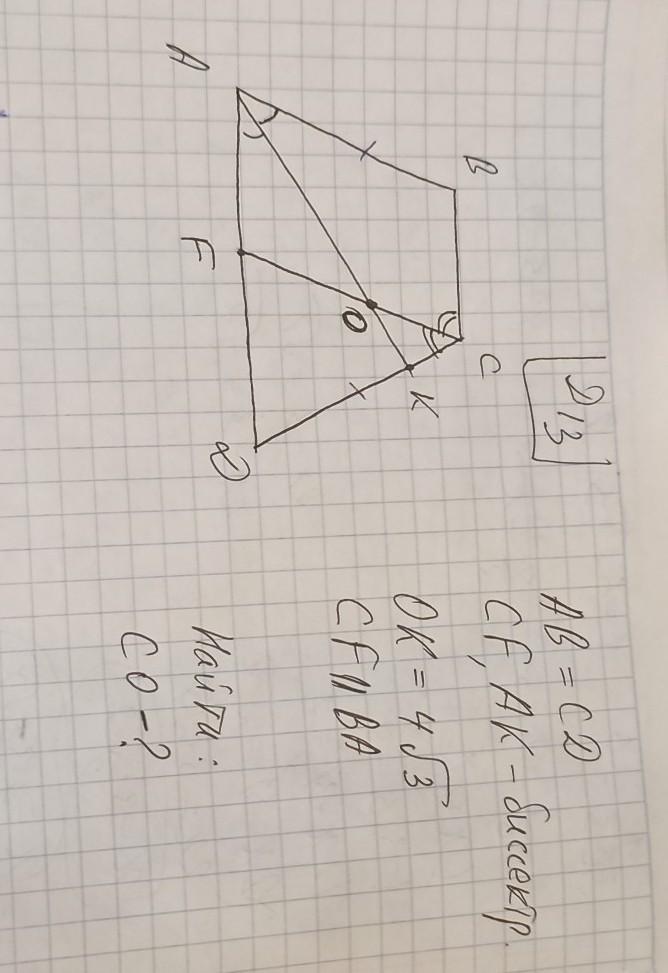
Рассмотрим △FCD: /_F=/_C так как /_F=/_ВCF, как внутринние разносторонние угли паралельних прямих и секущей и CD=DF. Тогда △FCD равнобедренний. Также FC||АВ и равна ей, так как находятся между паралельними прямими и так как у трапеции равни боковие сторони , то CD=CF=FD → △FCD- равносторонний и все угли в нем =60°, также /_А=60°, из свойства нашей трапеции.
Рассмотрим △АКD, он прямоугольний, так как /_D=60°, /_КАD=60/2=30° →/_АКD=90°
Рассмотрим △ОКС он прямоугольний и /_ОСК=60°
По теореме синусов ОС=ОК/sin60=4√3/(√3/2)=8
Обозначим половину острого угла при основании за "х".
Острый угол у точки F равен 2х, угол D тоже равен 2х.
Тогда угол FCD равен 180 - 4х.
С другой стороны, этот угол равен половине каждого из углов С и В.
(1/2)∠В = (180 - 2х)/2 = 90 - х.
Приравняем: 90 - х = 180 - 4х,
отсюда 3х = 180 - 90 = 90.
Угол х = 90/3 = 30 градусов, угол FCD = 90 - 30 = 60 градусов.
Это доказывает, что равнобедренный треугольник FCD является и равносторонним.
Треугольник СОК - прямоугольный.
СО = 4√3/cos 30° = 4√3/(√3/2) = 8.
Ответ: СО = 8.