У нижній Основі циліндра проведено хорду Яка знаходиться на відстані d від центра верхньої остови І яку видно із цього центра під кутом a. Відрізок який сполучає центр верхньої основи основи з точкою кола нижньої основи кут b. Знайдіть об’єм циліндра
Ответы
Ответ:
V = π•d³•cos²b•sinb/cos³(a/2)
Объяснение:
Перевод и дополнение: В нижнем основании цилиндра проведена хорда, которая находится на расстоянии d от центра верхней основы и которую видно из этого центра под углом a. Отрезок, соединяющий центр верхнего основания с точкой окружности нижнего основания, образует с плоскостью нижнего основания угол b. Найдите объем цилиндра.
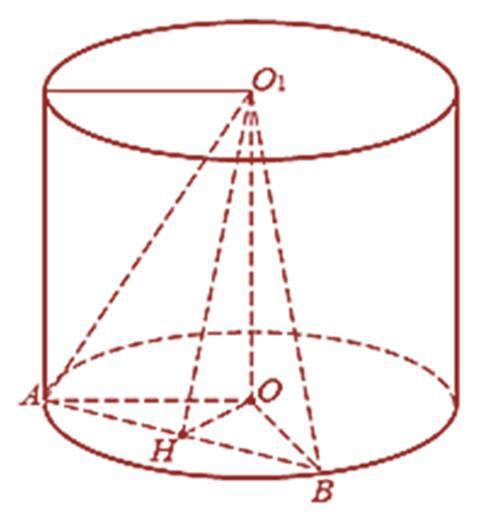
Дано (см. рисунок):
Цилиндр
О – центр (окружности) нижнего основания цилиндра
O₁ – центр (окружности) верхнего основания цилиндра
AB – хорда в нижнем основании цилиндра
∠AO₁B = a
∠O₁AO = ∠O₁BO = b
O₁H = d
Найти: объем цилиндра.
Решение.
В цилиндре высота h=OO₁ перпендикулярен к основаниям цилиндра и поэтому треугольники AOO₁ и BOO₁ являются прямоугольными.
Так как радиусы основания
OA = OB и ∠OAO₁ = ∠OBO₁ = b,
то прямоугольные треугольники AOO₁ и BOO₁ равны (признак равенства прямоугольных треугольников по катету и прилежащему острому углу). Тогда O₁A = O₁B, то есть треугольник AO₁B равнобедренный с основанием AB. Следовательно, отрезок O₁H является биссектрисой и высотой треугольника AO₁B. Отсюда
∠AO₁H = ∠AO₁B/2 = a/2 и O₁A = O₁H/cos(a/2) = d/cos(a/2).
Далее, в прямоугольном треугольнике AOO₁ определим катеты:
sinb = OO₁/O₁A или OO₁ = O₁A•sinb = d•sinb/cos(a/2);
cosb = OA/O₁A или OA = O₁A•cosb = d•cosb/cos(a/2).
Объём цилиндра V определяется через площадь основания S и высоту h по формуле:
V = S•h = π•OA²•OO₁ = π•(d•cosb/cos(a/2))²•d•sinb/cos(a/2) =
= π•d³•cos²b•sinb/cos³(a/2).