Предмет: Алгебра,
автор: AlexFab
Алгебра и начала математического анализа. Профильный уровень. 10 Класс.
Синус и косинус суммы и разности аргументов.
Помогите, пожалуйста! Буду очень благодарен. Фотографии с заданиями прикреплены ниже:
Приложения:

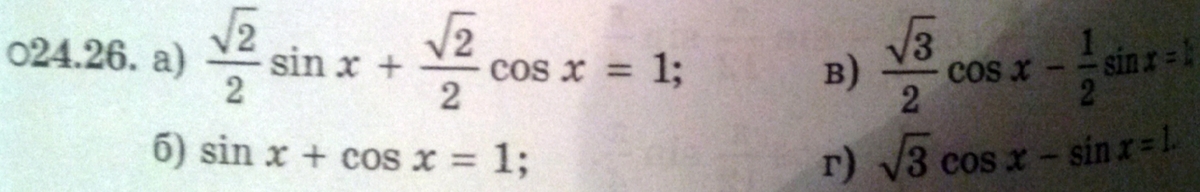
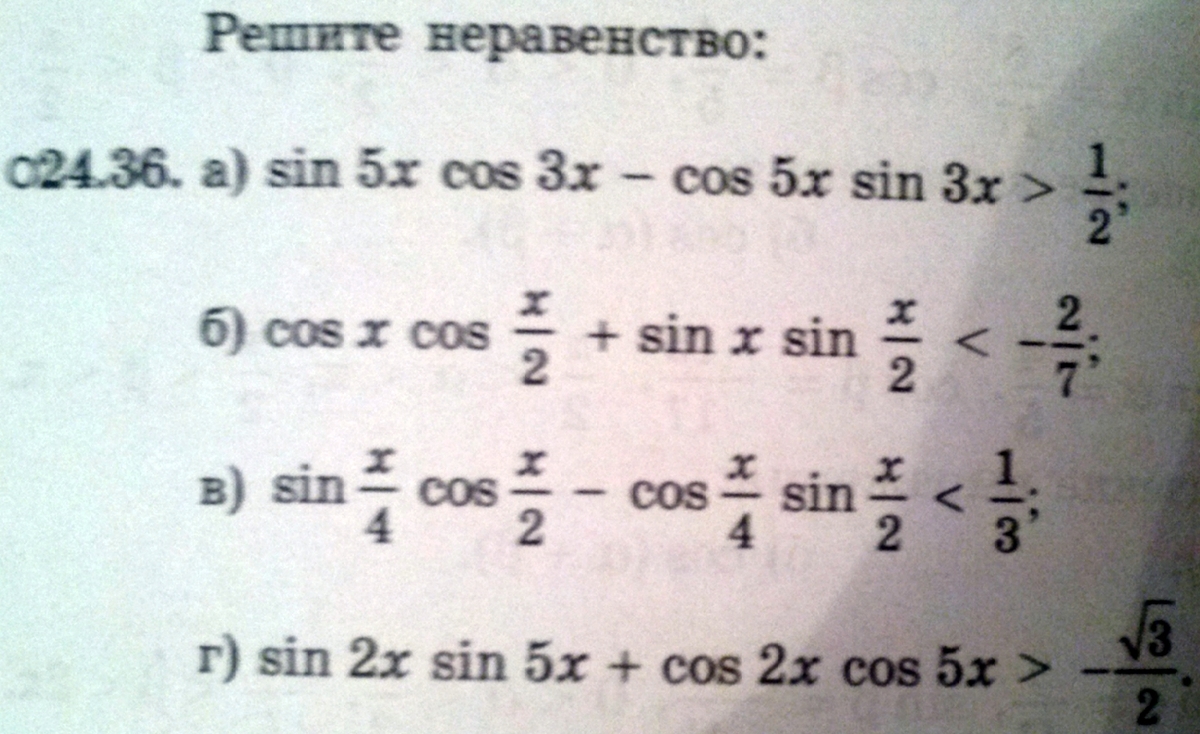
Ответы
Автор ответа:
0
24.23


Разделим на




24.26
a)Введем вспомогательный аргумент
 ,
, 






б) Разделим уравнение на
Введем доп. аргумент , такой что
 и
и 





в) Доп. аргумент такой, что
 и
и 
Далее по схеме
г)Разделим уравнение на 2
Введем доп. аргумент , такой как в в)
Далее по схеме
24.36
а)

[tex] frac{ pi }{12} + pi k
Разделим на
24.26
a)Введем вспомогательный аргумент
б) Разделим уравнение на
Введем доп. аргумент , такой что
в) Доп. аргумент такой, что
Далее по схеме
г)Разделим уравнение на 2
Введем доп. аргумент , такой как в в)
Далее по схеме
24.36
а)
[tex] frac{ pi }{12} + pi k
Похожие вопросы
Предмет: Информатика,
автор: miakhlov06
Предмет: Русский язык,
автор: dashka323232
Предмет: История,
автор: Alita666
Предмет: Биология,
автор: Позитиффчик13
Предмет: Алгебра,
автор: настюшка1276