помогите пожалуйста прошу умоляю
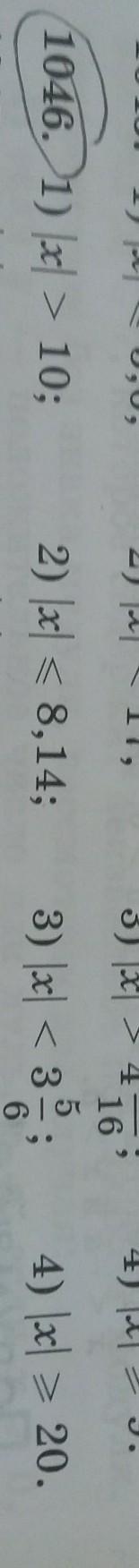
Ответы
Ответ:
Решение внизу
Пошаговое объяснение:
1)|x|>10
2) |x|≤8,14
3) |x|<3 5/6
4) |x|≥20
Решение:
1)|x|>10
По свойству функции модуля y=|x| рассмотрим два случая решения данного неравенства:
-x > 10 x > 10
x< -10
Отметим на числовой оси интервалы:
///////°------------°////////>x
-10 10
x ∈ (-∞;-10)∪(10;+∞)
Ответ: x ∈ (-∞;-10)∪(10;+∞)
2) |x|≤8,14
Рассматриваем два варианта решения:
-x≤8,14 x≤8,14
x≥ -8,14
Отметим на числовой оси интервалы:
\\\\\\\\\ * xxxxxxxx * //////////->x
-8,14 8,14
x ∈ [-8,14;8,14]
Ответ: x ∈ [-8,14;8,14]
3) |x|<3 5/6
Рассматриваем два варианта решения:
-x<3 5/6 x<3 5/6
x> -3 5/6
Отметим на числовой оси интервалы:
\\\\\\\\\ ° xxxxxxxx ° //////////->x
- 3 5/6 3 5/6
x ∈ (- 3 5/6;3 5/6)
Ответ: x ∈ (- 3 5/6;3 5/6)
4) |x|≥20
Рассматриваем два варианта решения:
-x≥20 x≥20
x≤-20
Отметим на числовой оси интервалы:
///////*------------*////////>x
-20 20
x ∈ (-∞;-20]∪[20;+∞)
Ответ: x ∈ (-∞;-20]∪[20;+∞)
Ответ:
В решении.
Пошаговое объяснение:
1) |x| > 10
Схема: |x| > 10 ⇒ х > 10
x < - 10
Решение неравенства: х∈(-∞; -10)∪(10; +∞), объединение.
Неравенство строгое, скобка круглая, а знаки бесконечности всегда с круглой скобкой.
2) |x| <= 8,14
Схема: |x| <= 8,14 ⇒ x >= -8,14
х <= 8,14
Решение неравенства: х∈[-8,14; 8,14], пересечение.
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда с круглой скобкой.
3) |x| < 3 и 5/6
Схема: |x| < 3 и 5/6 ⇒ x >= -3 и 5/6
х <= 3 и 5/6
Решение неравенства: х∈(-3 и 5/6; 3 и 5/6), пересечение.
Неравенство строгое, скобки круглые.
4) |x| >= 20
Схема: |x| >= 20 ⇒ х >= 20
x <= -20
Решение неравенства: х∈(-∞; -20]∪[20; +∞), объединение.
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда с круглой скобкой.