Предмет: Алгебра,
автор: alina00833
Помогите решить пожалуйста, срочно нужноо)
Приложения:

roff477:
помогите с алгеброй
Ответы
Автор ответа:
1
Ответ:
Приложения:
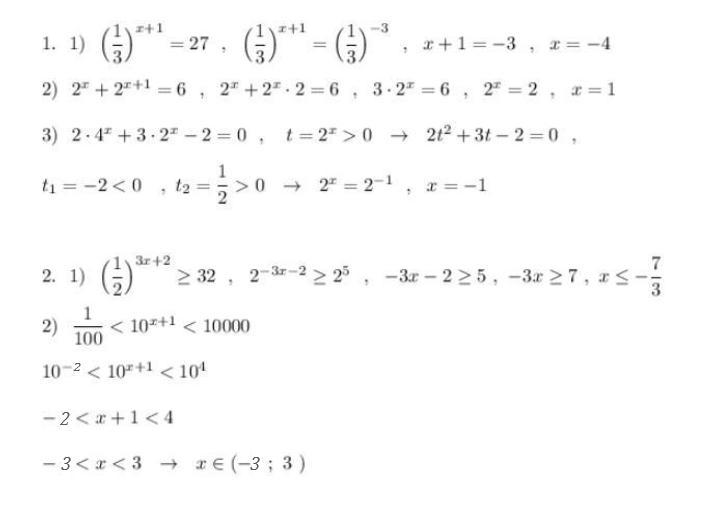
Можно скрин
Пожалуйста
Спасибо большое))
уже
Спасибо))
Выручили)
Помогите пожалуйста решить то что я сейчас выложила, очень нужно))
Похожие вопросы
Предмет: Русский язык,
автор: ONNovik
Предмет: Русский язык,
автор: МаринаФурсова
Предмет: Русский язык,
автор: azartik06
Предмет: Математика,
автор: Arishalovelove
Предмет: Английский язык,
автор: Burkhandinovaa