Question

Равнобедренные прямоугольные треугольники ABC и ADC имеют общую гипотенузу AC, равную 6 см, а их плоскости перпендикулярны. Найдите расстояние между точками B и D.

Answer 1

Ответ:

9√2 см

Объяснение:

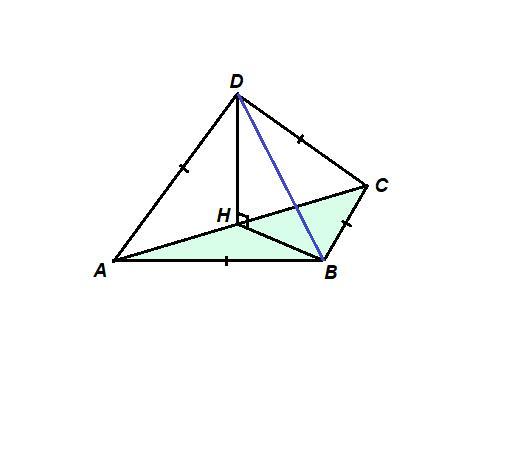
Проведем ВН⊥АС.

ΔАВС равнобедренный, тогда ВН - высота и медиана.

• Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.

ВН = 0,5 АС = 3 см

DH - медиана, а значит и высота равнобедренного прямоугольного треугольника ADC.

DH = 0,5 AC = 3 см

BH⊥AC, DH⊥AC, значит ∠BHD - линейный угол двугранного угла между плоскостями треугольников. Плоскости перпендикулярны, значит

∠BHD = 90°.

ΔBHD:  ∠BHD = 90°, по теореме Пифагора:

 $BD=\sqrt{BH^2+DH^2}=\sqrt{3^2+3^2}=\sqrt{9+9}=9\sqrt{2}$  см