Question

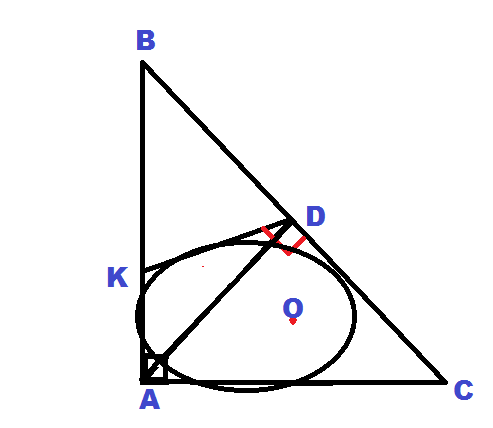
см рисунок 
Дан треугольник ABC: AB=15, AC=8, BC=17
точка K принадлежит AB так, что AK:KB=2:3
точка D принадлежит BC
KD перпендикулярен BC
окружность (центр O; R) описана вокруг треуг. AKD
R - ?
Решение:
Так как известны три стороны треугольника, то нужно проверить, является ли он прямоугольным. 289 = 225 + 64 (по т. Пифагора) --> да, является.
сторона AB = 15 и известно отношение AK и KB = 2:3
значит AK = 6, KB = 9
*окружность, в зависимости от вида треугольника, может располагаться по разному, а точнее её центр. Здесь треугольник AKD - тупоугольный (?). потому центр окружности расположен не внутри треугольника. Ведь четырехугольник AKDC, сумма углов в нем равна 360 градусов, а углы D и А = 90.[... ]
далее видно что есть подобные треугольники KBD и ABC, угол B - общий, а угол А = углу D = 90, т. е. треугольники подобны по первому признаку. 
AC : DK = BC : BK, вот такое отношение можно взять. 8:DK = 17:9, отсюда DK = 72/17
что дальше? как найти радиус?

Answer 1

АВ=15, АС=8, ВС=17, АВ=15=2х+3х=5х, х=3, АК=2*3=6, ВК=3*3=9, треугольник КВД подобен треугольнику АВС, как прямоугольные по острому углу В-общий, ВС/ВК=АК/КД, 17/9=8/КД, КД=72/17, ВС/ВК=АВ/ВД, 17/9=15/ВД, ВД=9*15/17=135/17, СД=ВС-ВД=17-135/17=154/17, АД в квадрате=(АВ в квадрате*СД/АС)+(АС в квадрате*ВД/ВС)-ВД*СД=(225*154/17 /17)+(64*135/17 /17)- (135/17)*(154/17))=(225*154+64*135-135*154)/(289)=22500/289, АД=150/17, треугольник АКД, полупериметр (р)=(КД+АК+АД)/2=(72/17+6+150/17)/2=(324/17)/2=162/17, площадьАКД=корень(р*(р-КД)*(р-АК)*(р-АД))=корень((162/17) *(162/17-72/17)*(162/17-6)*(162/17-150/17))=10497600/83521, площадьАКД=3240/289, радиус описанной=АК*КД*АД/(4*площадь)=(72*6*150/17*17) / (4*3240/289)=16200/3240 =5

Answer 2

чего не знаю, того не знаю