Предмет: Математика,
автор: mprevor
Задача Коши! Найти частные решения, удовлетворяющие указанным начальным условиям. :)
Приложения:
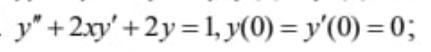
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
y'+2xy'+2y=1
Представим в виде:
2xy'+2y+y' = 1 - это неоднородное уравнение.
Сделаем замену переменных: y=u*v, y' = u'v + uv'.
2·u·v+u·v'+u'·v+2·x·(u·v'+u'·v) = 1
Выберем переменную v так, чтобы выполнялись условия:
1. u(2·v+2·v'·x+v') = 0
2. 2·u'·v·x+u'·v = 1
1. Приравниваем u=0, находим решение для:
2·v+2·v'·x+v' = 0
Представим в виде:
v' = -2·v/(2·x+1)
Преобразуем уравнение так, чтобы получить уравнение с разделяющимися переменными:
Интегрируя, получаем:
ln(v) = -ln(2·x+1)
v = 1/(2·x+1)
2. Зная v, Находим u из условия: 2*u'*v*x+u'*v = 1
2·u'·x/(2·x+1)+u'/(2·x+1) = 1
u' = 1
Из условия y=u*v, получаем:
y = u·v = (C+x)/(2·x+1)
Похожие вопросы
Предмет: Українська мова,
автор: MaxBrat4
Предмет: Русский язык,
автор: malik474
Предмет: Українська мова,
автор: Zalim867
Предмет: Русский язык,
автор: nufis
Предмет: Русский язык,
автор: enotic009