Предмет: Алгебра,
автор: llll97lllllll
Даю 50 баллов. Решите номер 636 (в) с объяснением.
Приложения:
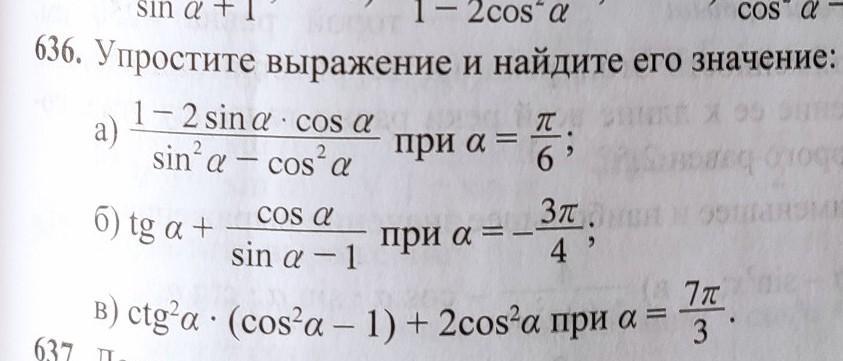
Ответы
Автор ответа:
2
Ответ:
llll97lllllll:
как вы из cos a =7Pi/3 получили cos a = (3Pi * Pi/3)?
у меня такого не написано ... ,но 7П/3=2П+(П/3) - это арифметика ....
В в) сумма квадратов косинуса и синуса в чеслителе дает 1, у вас она изчезла
где вы видите сумму в числителе ? там произведение cos^2x и sin^2x , делится всё на sin^2x , сокращаем потом sin^2x
Вторая строчка после второго =
Похожие вопросы
Предмет: Русский язык,
автор: dashafigur
Предмет: Русский язык,
автор: ayim1
Предмет: Другие предметы,
автор: курлай
Предмет: Математика,
автор: Zarina01020304
Предмет: Алгебра,
автор: лина6661