помогите пж
пж пж пж пж
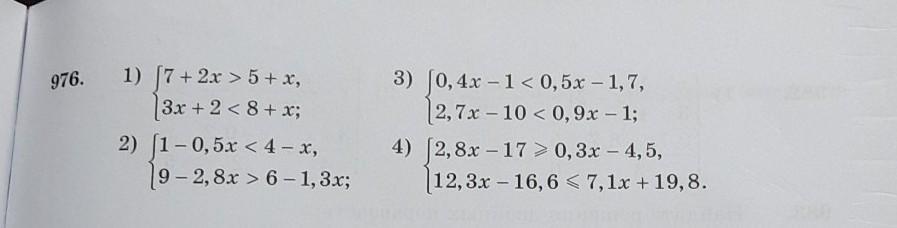
Ответы
Ответ:
В решении.
Пошаговое объяснение:
Решить системы неравенств:
1) 7 + 2х > 5 + x
3x + 2 < 8 + x
2x - x > 5 - 7
3x - x < 8 - 2
x > -2
2x < 6
x > -2
x < 3
Решение первого неравенства х∈(-2; +∞);
Решение второго неравенства х∈(-∞; 3);
Решение системы неравенств х∈(-2; 3), пересечение.
Неравенства строгие, скобки круглые.
2) 1 - 0,5х < 4 - x
9 - 2,8x > 6 - 1,3x
-0,5x + x < 4 - 1
-2,8x + 1,3x > 6 - 9
0,5x < 3
-1,5x > -3
x < 3/0,5
x < -3/-1,5 знак неравенства меняется при делении на минус
x < 6
x < 2
Решение первого неравенства х∈(-∞; 6);
Решение второго неравенства х∈(-∞; 2);
Решение системы неравенств х∈(-∞; 2), пересечение.
Неравенства строгие, скобки круглые.
3) 0,4х - 1 < 0,5x - 1,7
2,7x - 10 < 0,9x - 1
0,4x - 0,5x < -1,7 + 1
2,7x - 0,9x < -1 + 10
-0,1x < -0,7
1,8x < 9
x < -0,7/-0,1
x < 9/1,8
x > 7 знак неравенства меняется при делении на минус
x < 5
Решение первого неравенства х∈(7; +∞);
Решение второго неравенства х∈(-∞; 5);
Решение системы неравенств х∈∅, решений нет.
Неравенства строгие, скобки круглые.
4) 2,8x - 17 >= 0,3x - 4,5
12,3x - 16,6 <= 7,1x + 19,8
2,8x - 0,3x >= -4,5 + 17
12,3x - 7,1x <= 19,8 + 16,6
2,5x >= 12,5
5,2x <= 36,4
x >= 12,5/2,5
x <= 36,4/5,2
x >= 5
x <= 7
Решение первого неравенства х∈[5; +∞);
Решение второго неравенства х∈(-∞; 7];
Решение системы неравенств х∈[5; 7], пересечение.
Неравенства нестрогие, скобки квадратные, а при знаках бесконечности скобки всегда круглые.