Question

Диагональ параллелограмма делит острый угол, из вершины которого она выходит, в отношении 1:3. Найди меньший из углов между этой диагональю и сторонами параллелограмма, если тупой угол параллелограмма равен 120°.

Answer 1

Ответ:

∠BAC = 15°

Объяснение:

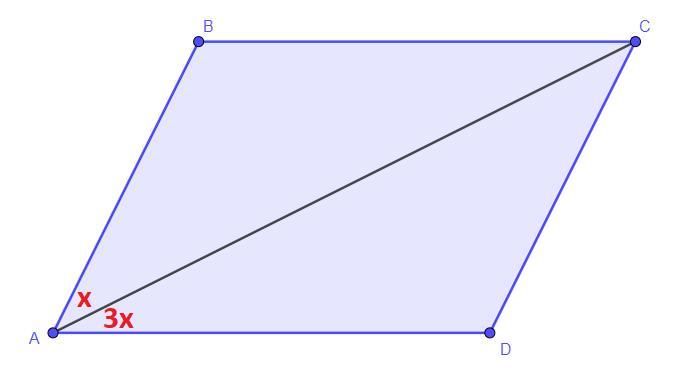
Дано: ∠ABC = 120°, ∠BAC : ∠CAD = 1 : 3

Найти: ∠BAC - ?

Решение: Так как по определению параллелограмма BC║AD, то угол

∠ABC и ∠BAD внутренние односторонние углы при параллельных прямых и секущей, тогда по теореме ∠ABC + ∠BAD = 180° ⇒ ∠BAD = 180° - ∠ABC =

= 180° - 120° = 60°. Так как по условию ∠BAC : ∠CAD = 1 : 3, то для углов

∠BAC и ∠CAD введем коэффициент пропорциональности x, тогда

∠BAC = x, ∠CAD = 3x.

∠BAC + ∠CAD = ∠BAD

x + 3x = 60°

4x = 60°|: 4

x = 15°.

∠BAC = x = 15°.