Предмет: Математика,
автор: nikita1creative
1)найти производную элементарных функций
2)исследовать функцию на экстремум
3) найти наибольшую и наименьшую значение функции
Приложения:
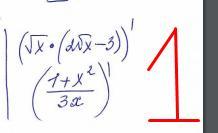
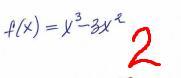
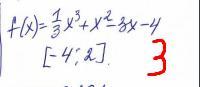
Ответы
Автор ответа:
1
1.
2.
Ответ: 0 и 2 - экстремумы
3.
-3 - точка максимума
1 - точка минимума
проверим эти значения, а заодно границы промежутка, подставиив в функцию
получаем
5 - максимальное значение
-5 2/3 - минимальное
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Сырым2
Предмет: Другие предметы,
автор: dino05
Предмет: Русский язык,
автор: пороль4
Предмет: Английский язык,
автор: Luba221103