Предмет: Геометрия,
автор: lizanime40
СРОЧНО ПОМОГИТЕ, ВОПРОС ЖИЗНИ И СМЕРТИ
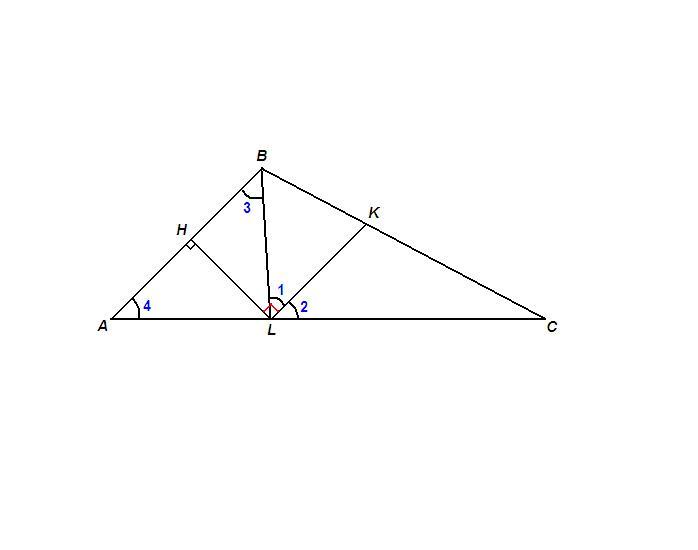
В треугольнике ABC на стороне AC выбрана точка L и проведены высота LH треугольника ABL и бессектриса LK треугольника BLC оказалосб, что угол KLH прямой. Найдите AB если AH =6
Нужно с решением
Ответы
Автор ответа:
3
Ответ:
12
Объяснение:
По условию ∠KLH = 90°, т.е. KL⊥LH,
LH⊥AB, так как LH высота ΔABL, следовательно
KL║AB как перпендикуляры к одной прямой (LH).
∠1 = ∠3 как накрест лежащие при пересечении параллельных прямых KL и AB секущей BL,
∠2 = ∠4 как соответственные при пересечении параллельных прямых KL и AB секущей АС.
Так как ∠1 = ∠2 (LK - биссектриса треугольника BLC), то и
∠3 = ∠4.
В треугольнике ABL равны два угла, прилежащие к стороне АВ, значит он равнобедренный с основанием АВ.
В равнобедренном треугольнике высота, проведенная к основанию, является медианой, значит
АВ = 2АН = 2 · 6 = 12.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: AmStaFF424
Предмет: Русский язык,
автор: celena77
Предмет: Русский язык,
автор: vasilisagerasi1
Предмет: Музыка,
автор: ahmedatabaev884
Предмет: Математика,
автор: georgiy80