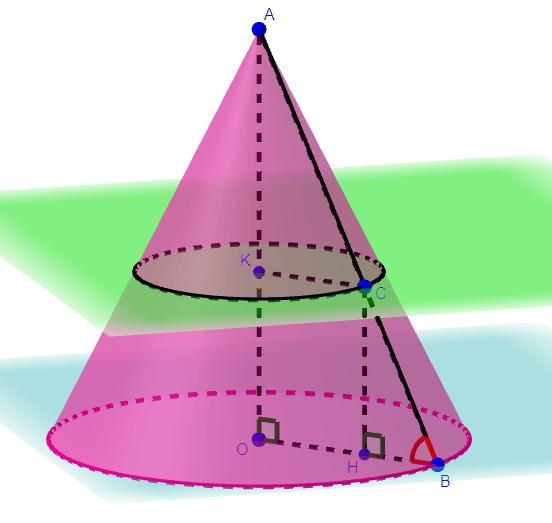
Образующая усеченного конуса равна 2 см и наклонена к плоскости основания под углом 60. Радиус меньшего основания усеченного конуса равен 1. Найдите радиус большего основания этого усеченного конуса
Ответы
Ответ:
Объяснение:
Дано: BC = 2 см, ∠CBO = 60°, KC = 1, OK - ось конуса
Найти: OB - ?
Решение:
Осевым сечением усеченного конуса является трапеция, тогда KOBC - трапеция, а так как по условию OK - ось конуса, а ось конуса является и высотой по свойствам усеченного конуса, тогда KOBC - прямоугольная трапеция.
Проведем из точки C на сторону OB высоту трапеции в точку H. Так как CH ⊥ OB по построению, и OK ⊥ OB, то по теореме OK║CH. KOBC - трапеция ⇒ её основания параллельны, KC║OB. Так как KC║OB и OK║CH, то по определению четырехугольник KOHC - параллелограмм.
Так как KOHC - параллелограмм ⇒ OH = KC (по свойству параллелограмма). Так как CH ⊥ OB по построению ⇒ ΔCHB - прямоугольный и по по определению тригонометрических функций в прямоугольном треугольнике:.
По основному свойству отрезка:
OB = OH + BH = KC + BH = 1 + 1 = 2.