Question

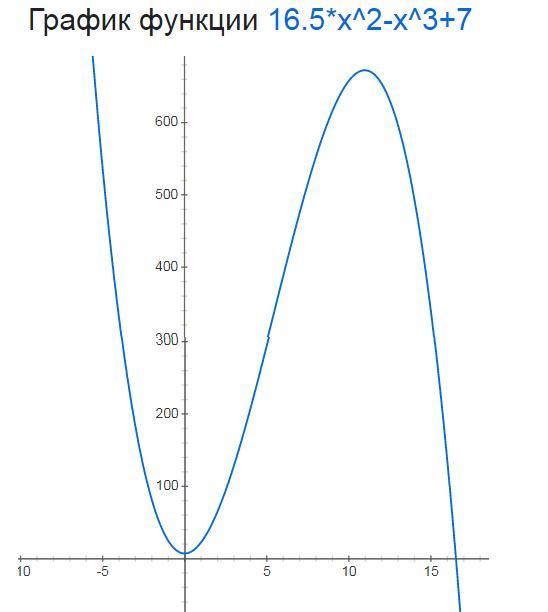
найдите точку минимума функции y=16.5x^2-x^3+7

Answer 1

Ответ:

$y=16,5x^2-x^3+7\\\\y'=33x-3x^2=3x\, (11-x)=0\ \ \to \ \ \ x_1=0\ ,\ x_2=11\\\\znaki\ y':\ \ \ ---(0)+++(11)---\\\\{}\qquad \qquad \qquad \searrow \ \ \,(0)\ \ \, \nearrow \ \ (11)\ \ \ \searrow \\\\x_{min}=0\ \ ,\ \ y_{min}=y(0)=7\ \ ,\ \ \ A(\ 0\, ;\, 7\, )$

Answer 2

Ответ:

Объяснение:

y=16.5x^2-x^3+7

y’=16.5*2x-3x^2=33x-3x^2=0

3x(11-x)=0

x1=0 ; x2=11

Нанесем найденные значения х на числовую прямую и определим знаки  производной на интервалах

По свойству квадратичной функции так как коэффициент при х^2

-3<0 то ветки параболы направлены вниз тогда значения производной на интервалах будут иметь знаки (-) ( +) ( -)  

     ----------------0-----------------11--------------->

 Y’       -                     +                       -  

В точке х=0 производная меняет знак с – на +  

= >  В точке х=0 – минимум функции

Y(0)=0-0+7=7

(0;7) точка минимума