Предмет: Алгебра,
автор: angelinakim080
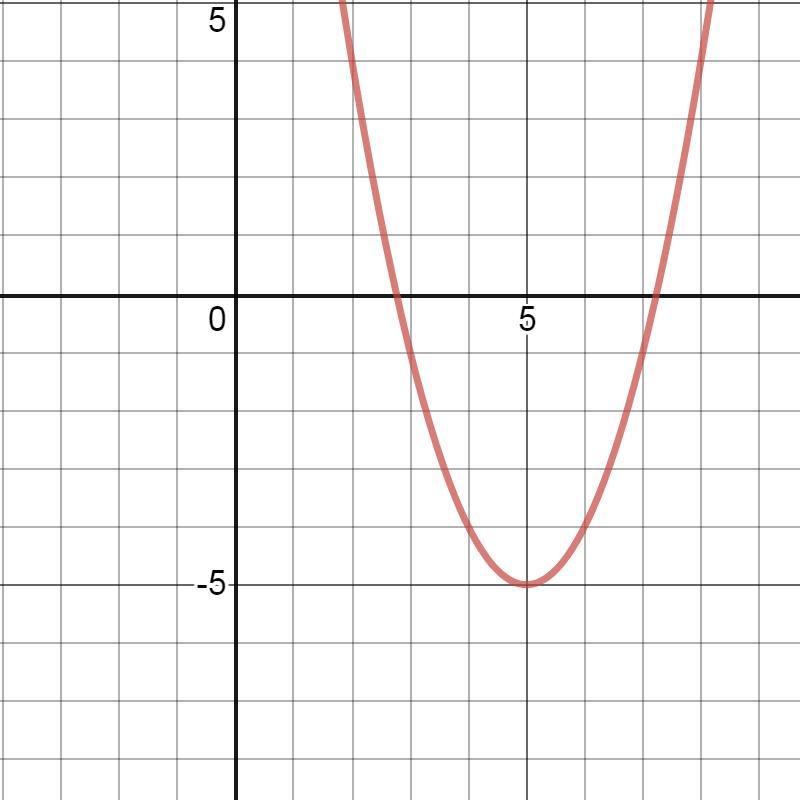
Дана функция у =х^2-10х+20 а Запишите координаты вершины параболы B Запишите ось симметрии параболы c Найдите точки пересечения графика с осями координат постройте график функции Определите в каких четвертях находится график функции
fatimakariimova:
А можно решение где y=x²-8x+12 а остальное так же
Ответы
Автор ответа:
31
Объяснение:
График находится в 1-й, 2-й и 4-й четвертях.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Биология,
автор: NUrs726
Предмет: Математика,
автор: Pavel2208Pasha
Предмет: Окружающий мир,
автор: ас123234
Предмет: Алгебра,
автор: Tysyapp