Предмет: Геометрия,
автор: SebastianMihaels
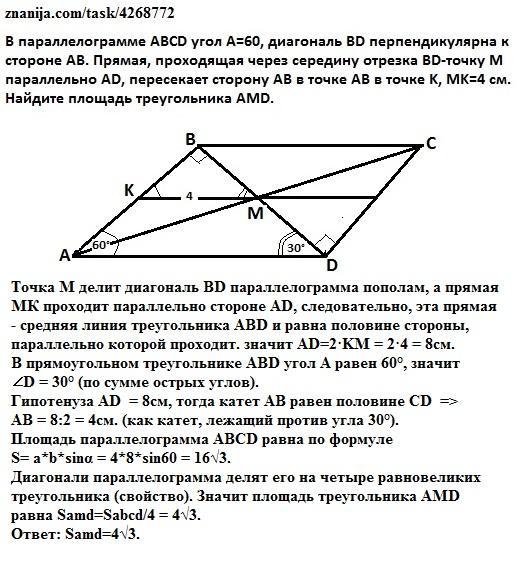
В параллелограмме ABCD угол A=60, диагональ BD перпендикулярна к стороне AB. Прямая, проходящая через середину отрезка BD-точку М параллельно AD, пересекает сторону AB в точке AB в точке K, MK=4 см. Найдите площадь треугольника AMD.
Помогите пожалуйста:3
Приложения:

Ответы
Автор ответа:
0
Точка М делит диагональ ВD параллелограмма пополам, а прямая МК проходит параллельно стороне AD, следовательно, эта прямая - средняя линия треугольника АВD и равна половине стороны, параллельно которой проходит. значит AD=2·KM = 2·4 = 8см.
В прямоугольном треугольнике АВD угол А равен 60°, значит ∠D = 30° (по сумме острых углов).
Гипотенуза AD = 8см, тогда катет АВ равен половине CD => АВ = 8:2 = 4см. (как катет, лежащий против угла 30°).
Площадь параллелограмма АВСD равна по формуле
S= a*b*sinα = 4*8*sin60 = 16√3.
Диагонали параллелограмма делят его на четыре равновеликих треугольника (свойство). Значит площадь треугольника AMD равна Samd=Sabcd/4 = 4√3.
Ответ: Samd=4√3.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: dazzlinggerl
Предмет: История,
автор: Janech2
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Биология,
автор: Wagon