Question

Найдите радиусы окружностей вписанной и описанной около равнобедренного треугольника,в котором высота,опущенная к основанию равна 20 см,а отношение основания к боковой стороне равно 4:3

Answer 1

Ответ:

8см- радиус вписанной окружности

18см- радиус описанной окружности

Решение:

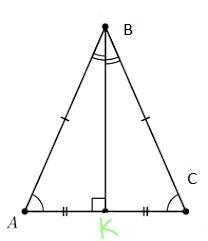
Дано: ΔАВС, АВ=ВС, ВК⊥АС, ВК=20см, АС:АВ=4:3

Найти: R-? r-?

Решение:

В равнобедренном треугольнике высота, опущенная на основание, одновременно является и биссектрисой угла и медианой, проведенной к основанию.

Пусть основание АС=4х , а АВ=ВС=3х,

Рассмотрим Δ АВК, где ∠К=90°, АВ=3х, АК=1/2 АС=2х

По теореме Пифагора

АВ²=АК²+ВК²;

(3х)²=(2х)²+ 20²;

9х²- 4х²=400;

х²=400:5;

х=√80=4√5(см)

АВ=ВС=3х=3*4√5см=12√5 см

АС=4х=4*4√5см=16√5см.

$S_{ABC}=\frac{1}{2}AC*BK=\frac{16\sqrt{5} *20}{2} =160\sqrt{5}$ (см²)

$S_{ABC}=pr;\\160\sqrt{5} =\frac{2*12\sqrt{5}+16\sqrt{5} }{2}*r; \\\\r=\frac{160\sqrt{5} }{20\sqrt{5} } =8$(cм)- радиус вписанной окружности)

$R=\frac{AB*DC*AC}{4S} =\frac{(12\sqrt{5})^2*16\sqrt{5} }{4*160\sqrt{5} }=\frac{144*5}{4*10}= 18$(см)- радиус описанной окружности