Предмет: Алгебра,
автор: boyg21961
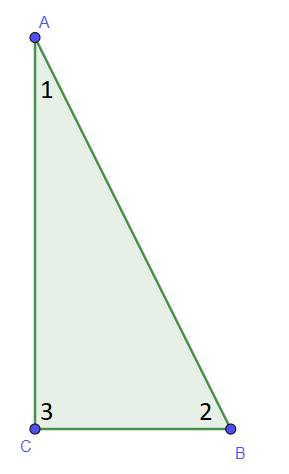
В треугольнике первый угол меньше второго на 30° и больше третьего на 30°. Сумма длин наибольшей и наименьшей сторон треугольника равна 24. Найди длину наибольшей стороны треугольника.
Ответы
Автор ответа:
1
Ответ:
AB = 16
Объяснение:
Дано: ∠2 = ∠3 - 30°, ∠2 = ∠1 + 30°, AC + AB = 24
Найти: AB - ?
Решение: ∠2 = ∠3 - 30° ⇒ ∠3 = ∠2 + 30°.
∠2 = ∠1 + 30° ⇒ ∠1 = ∠2 - 30°.
По теореме про сумму углов треугольника:
∠1 + ∠2 + ∠3 = 180°
∠2 - 30° + ∠2 + ∠2 + 30° = 180°
3∠2 = 180°|:3
∠2 = 60°.
∠1 = ∠2 - 30° = 60° - 30° = 30°.
∠3 = ∠3 + 30° = 60° + 30° = 90°.
По теореме против большего угла лежит большая сторона, тогда наибольшая сторона треугольника AB, так как лежит напротив угла ∠ACB, а наименьшая AC, так как лежит напротив угла ∠ABC.
(∠BAC < ∠ABC < ∠ACB; 30° < 60° < 90°).
По теореме в прямоугольном треугольнике против угла в 30 градусов лежит катет, равный половине гипотенузы, тогда AC = 0,5AB.
AC + AB = 24
0,5AB + AB = 24
1,5AB = 24|:1,5
AB = 16.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: pupsik1313
Предмет: Литература,
автор: prostovadik196
Предмет: Русский язык,
автор: Nigishaa
Предмет: Алгебра,
автор: kalinkinmaksim
Предмет: Математика,
автор: Purple1111