Question

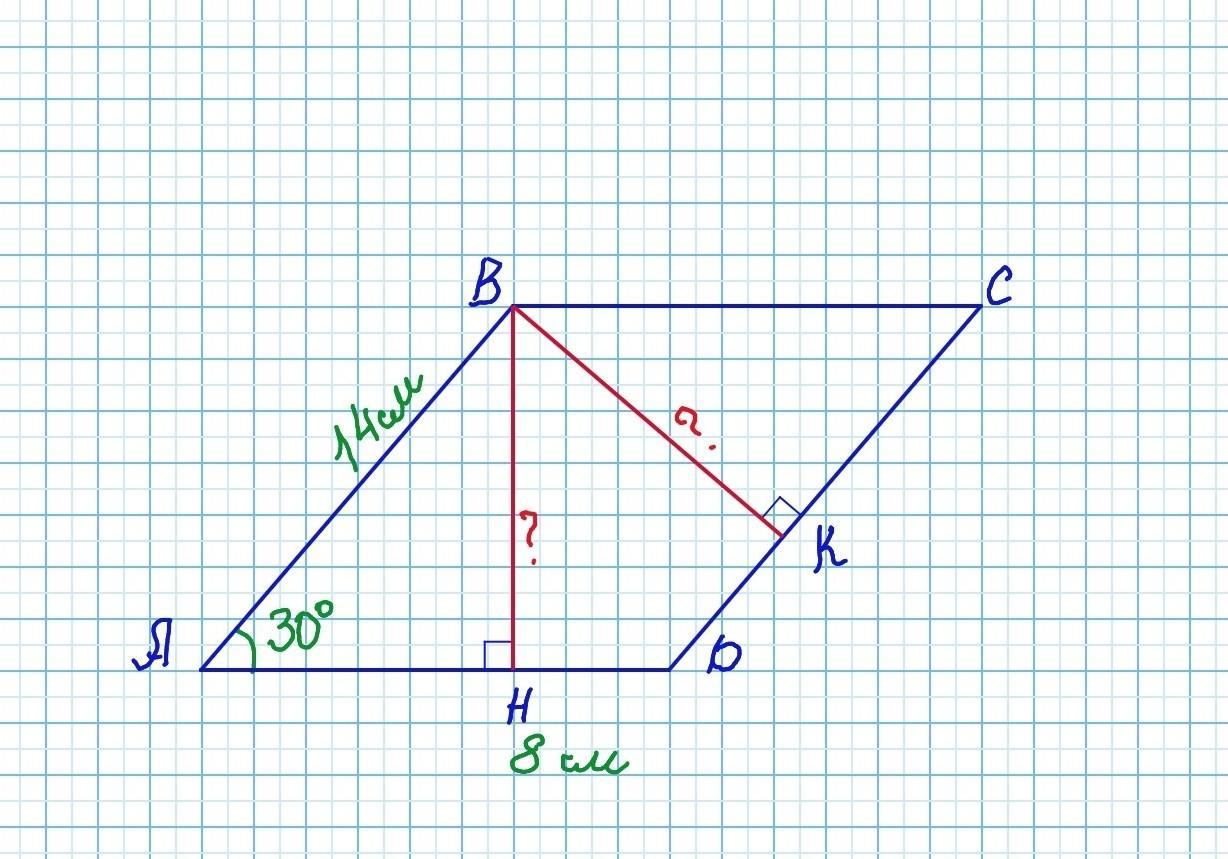
В параллелограмме ABCD стороны AB = 14 см и AD = 8 см. BH и BK – высоты параллелограмма, проведенные к сторонам AD и DC соответственно. Если угол между сторонами равен 30°, то найди площадь и высоты параллелограмма.
​

Answer 1

Ответ:

S=56 см².

ВН = 7см.

BK = 4см

Объяснение:

Дано: ВН⟂AD, BK⟂DC, AB=14 см, AD=8 см, ∠A=30°.

Найти: S(ABCD), BH, BK.

1) Площадь параллелограмма вычисляется по формуле:

S=a•b•sin∠A,

где а и b - стороны параллелограмма, ∠A - угол между ними.

S= 14•8•sin30° = 112•½ = 56 см².

2) Рассмотрим прямоугольный треугольник АВН(∠Н=90°)

Катет, лежащий напротив угла в 30° равен половине гипотенузы:

ВН = ½•АВ = ½•14 = 7см.

3) Площадь параллелограмма также можно найти по формуле:

S = a•h, где а - сторона параллелограмма, h - высота, проведенная к этой стороне.

Так как противоположные стороны параллелограмма равны, то DC = AB = 14см.

Тогда можем найти высоту ВК, проведённую к стороне DC:

$BK= \dfrac{S}{DC} = \dfrac{56}{14} = 4$см