Предмет: Алгебра,
автор: monteshadows
Найти вторую производную функции Y:
Приложения:
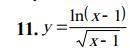
Ответы
Автор ответа:
2
Ответ:
Похожие вопросы
Предмет: Алгебра,
автор: УченикНужнаПомощь
Предмет: Русский язык,
автор: vernickiforova
Предмет: Геометрия,
автор: anna40890
Предмет: Математика,
автор: dasha121haust
Предмет: Русский язык,
автор: суслик53