Предмет: Геометрия,
автор: JakeyRO
50 баллов В прямоугольном треугольнике к гипотенузе проведены медиана и высота. Угол между ними равен 20градусов. Определите величину каждого из острых углов данного прямоугольного треугольника.
Ответы
Автор ответа:
8
Ответ:
∠А = 35°
∠В = 55°
Объяснение:
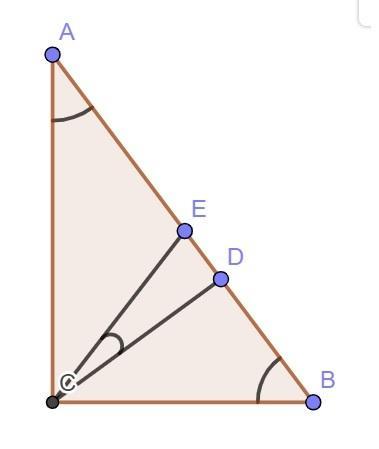
т.к. CD высота то ∠CDE - прямоугольный, где ∠ECD = 20°
тогда из прямоугольного ΔCED находим
∠CED = 180° - 90° - 20° = 70°
т.к. медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. то СЕ = ЕВ
Значит ΔСЕВ равносторонний с вершиной ∠СЕВ = 70°
и углы при основании равны, значит
∠ЕСВ =∠ЕВС = (180° - 70°)/2 = 55°
т.о. нашли угол В = 55°
теперь из ΔАВС найдем угол А
∠А = 180° - ∠С - ∠В = 180° - 90° - 55° = 35°
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: mudrajj
Предмет: Другие предметы,
автор: elvinka1241
Предмет: Математика,
автор: 55584
Предмет: Математика,
автор: ден910
Предмет: Математика,
автор: ysyncinovp4g8zy